[machine learning] day16-one variable regression
Machine Learning에 대한 내생각
machine learning이란 단어
“machine"이란?
Machine Learning이라는 분야에서는 사용되는 용어가 있다. 기존에 어디서 보았던 용어도 machine learning분야에서는 다른 용어로 사용된다. “Machine Learning"이란 단어를 생각해보자. machine learning에서 “machine"은 turing과 church의 관점에선 function이다. 입력이 주어지면 출력이 나오는 function이다. 예를 들어, 1차방정식 y= 2x + 4는 machine이고, 이 기계에 1을 넣으면 6이나온다. 이런 값이 나오는 이유는 입력되는 data 1과 machine이 가진 계수와 연산자에 의한 결과다. machine이 가진 계수와 연산자들은 function형태고, 이것을 model이라고 부른다. 6이란 결과는 기계가 만들어내는 값이다. 이 값을 예측값이라고 한다. 그런데 여기서 한가지! turing과 church혹은 godel이 제시했던 recursion한 machine조차도 deductive한 rule을 사용한다는 것이다. 이 말은 y = 2x + 4라는 기계에서는 big data가 필요 없다는 뜻이다. 원하는 data를 입력하면 원하는 예측치가 확정적으로 나오기 때문이다. model이 고정적이다. model이 고정적이기 때문에 learning을 할 필요도 없다. model을 만들기 위해 big data가 필요없다는 뜻이다. 고정적인 model에선 그렇다. 반면에 “machine learning"에서의 machine은 inductive한 rule을 사용한다. y=2x +4라는 기계의 계수들이 data에 의해 변한다. 양질의 그리고 많은(big) data가 제공될때의 function과 그렇지 않을때의 function은 다른 model을 갖는 기계가 된다.
“Learning"이란?
“machine learning"에서의 machine의 model은 data에 의해 규정되고 변한다. Machine의 model을 update하는 것을 “Learning"이라고 부른다. machine을 구성하는 부품들이 있고, 이를 update하듯이, function을 구성하는 부품인 계수가 있고 계수를 update하는데, 이것이 learning이다. 예를 들어서 1차방정식 y=2x+4가 있다고 하면, 2와 4는 function을 이루는 부품들로 볼수 있다. 여기서 계수를 update하는 것이 learning이다. 예를 들어, y=2x+4를 update해서 y = 4x+1 로 변경한다면, 그것은 learning이 이루어진 것이다. model이 1차방정식이나 2차방정식 같은 경우에는 계수값을 update하는게 learning이지만,모든 경우가 그런것은 아니다. 어떤 경우에는 model내에 중심값이라는 변수를 유지하고, 이 변수를 update하는게 learning이 되기도한다. clustering같은 경우가 있다. 또한 확률론으로 machine을 본다면, 베이지언 확률이 update하는 rule이 된다.
“Machine Learning"이란
위에서 “machine"과 “learning"에 대해서 알아봤다. “Machine Learning"이라고 쓴 이유는 machine learning의 process를 말할려고 한다. machine이란 function이고 function의 결과값은 estimate value라고 했다. machine learning이 사용되면 machine은 data를 입력으로 받아서 estimate value로 예측을 한다. “machine"의 하는일이다. 그다음은 “Learning"이 시작된다. Learning은 model의 계수를 update한다. cost function, loss function으로 부르는 계수의 값을 update하는 함수가 따로 존재한다. update된 계수로 다시 machine은 예측을 하고, 예측된 값을 가지고 다시 update를 한다. 이 과정이 계속된다.
Machine Learning 용어들
Supervised learning
learning의 종류중 하나다. learning은 model의 어떤 parameter를 update하는 것이다. 계수를 update할 수도 있고 어떤 중심값을 update할 수 있다. update하는 기준은 learning마다 다르다. supervised learning은 정답인 data혹은 정답인 label이 있어서 계수를 정답에 가깝게 update한다. regression과 classification이 supervised learning이라고 하는지는 잘 모르겠다. 다만 예측한다면, regression과 classification 모두 정답이 있는 data를 처리하기 때문일 것이다. 여튼 regression과 classification이 해결하는 model들은 1차방정식과 같은 형태이다. 즉 model에는 계수(parameter)가 있어서, 그 계수를 정답과의 비교를 통해 update할수가 있다. 예를 들면, 어떤 data가 과거의 환자들의 몸무게,키, 수명을 제공하면 이 data에는 수명을 예측하기 때문에 수명이 정답으로 있는 data와 그렇지 않은 data가 주어진다. 이미 죽은 사람들의 data라서 정답에 해당하는 수명이 있다. 따라서 모델의 계수를 update해서 정답에 가까운 값이 나오게 학습시키는 것을 말한다. 이렇게 learning이 끝나면 살아있는 사람의 data로 수명을 예측할수 있다. 수명은 우리가 알고싶은 값이였고, 학습시에는 주어졌다. 반면 test시에는 정답이 주어지지 않는다.
Unsupervised learning
machine의 model이 1차방정식,고차방정식,삼각함수,지수함수, 로그함수, 연립방정식과 같은 형태가 아니다. supervised learning은 data가 주어지면, data에 대한 정답이 있어서 그 오차를 줄여서 최대한 정답에 가깝게 계수를 learning하는 것과 달리, unsupervised learning은 data에 정답이 없다. 따라서 오차도 없다. data가 가진 값을 임의의 평균과의 거리를 계산할 뿐이다. machine의 model은 거리 계산식과 평균변수가 들어있다. data가 들어오면 거리를 계산한다. 평균을 update한다. data가 들어오면 평균만을 업데이트한다. 따라서 supervised learning처럼 정답인 data와 정답이 없는 data로 나눌 필요가 없다. 모든 data를 입력해서 data의 평균만을 update한다. clustering, kmeans algorithm같은 방식들이 있다. 그런데 이런 machine은 개개의 data에 대해서 예측을 할 수 있는지는 모르겠다.
Linear model
machine은 function이고 function식이 model이라고 했다. function은 1차방정식도 function이고 2차방정식도 function, 지수,log, 삼각함수, 연립방정식도 function이다. 어떤 function식을 사용하는냐는 어떤 model을 사용하느냐?라는 말과 같다. linear model은 1차방정식이나 1차 연립방정식이 model이란 뜻이다.
Regression vs classification
machine은 function이고, function은 입력 data를 받아서 결과를 내보낸다. 내보내는 그 결과값을 machine learning에서는 예측값 or target variable이라고 부른다. 강사는 예측값의 종류에 따라서 regression과 classification으로 나눌수 있다고 한다. 예를 들면, 몸무게,키와 같은 입력에 대해서 예상수명과 같은 실수값을 예측한다면 regression이고, 몸무게, 키 입력에 대해서 신체검사 A,B,C 등을 예측한다면, 그것은 classification이라고 말한다. 그런데 출력값에 따라서 판단하는거 같진 않다. 처음 machine을 설계를 할때 어떤 문제인지를 파악할 것인데, 즉, 알고 싶은것, 예측하고 싶은것에 맞추어 machine을 만들텐데, 그때 regression, classification이 결정된다고 본다. 즉 machine을 만들때 정해지기 때문에, regression machine과 classification machine로 말해지는 것같다.
Linear Regression
참조: 이강의는 Andrew ng교수의 machine learning 강의를 참조한 듯 보인다.
개요
Supervised learning을 사용하는 classification과 regression중에 이 강좌에서는 regression을 사용한다. 아래는 강의의 내용을 요약해서 위에 machine learing에 대핸 내생각과 중복되는 내용이 있을 수 있다.
Linear Regression with one variable
Linear Regression with one variable의 의미
-
Linear란
Linear는 직선의 방정식을 말한다. y= ax +bx +cx +…+z의 꼴을 갖는 1차함수형을 말한다. machine의 model이 linear 방정식으로 되어 있는 경우를 뜻한다.
-
Regression
machine의 출력값, function의 함수값이 real-value인것을 뜻한다. estimate value가 real value다. 만일 estimate value가 discrete value면 classification이다.
regression의 예: 사람의 수명을 예측하는 문제, 1차 방정식으로 model을 만들고, 그 모델로 사람의 수명을 예측했는데, 38살이 나왔다거나, 45.2개월이 나왔다고 하면, 이것은 linear regression을 사용한것이다.
classification의 예: 신체검사 데이터로 간암이다, 아니다를 판단하는 문제 1차방정식으로 model을 만들고 그 모델의 결과값으로 yes or no를 예측하는 문제의 경우는 classification이다.
-
with one variable
supervised learning의 경우, data는 두 종류가 있다. training과 test다. training data에는 data의 종류와 정답이 있다.
강의 시작
one-variable linear regression
data
다음과 같은 data가 있다고 하자.
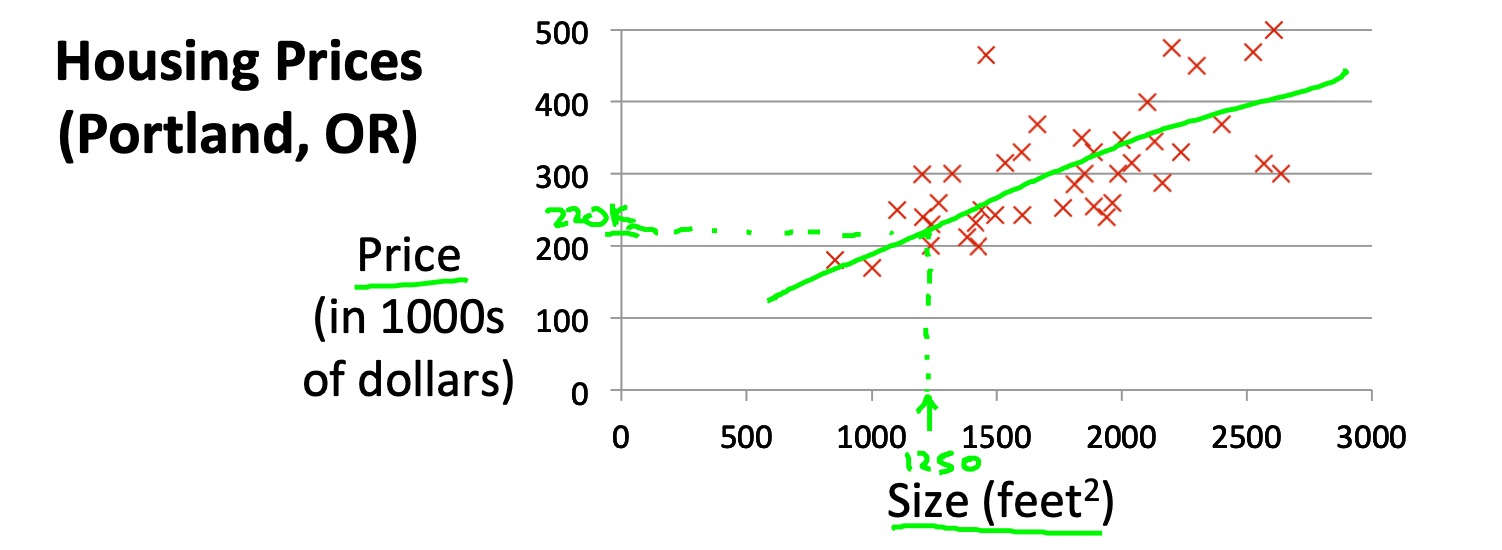
Figure 1: housing prices
| size of square of feet(x) | price($) in 1000’s(y) |
|---|---|
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
| … | … |
m = Number of training examples
x's = "input" variable / features
y's = "output" variable / "target" variable
집 평수에 따른 portland의 집값이다. data는 표로 주어진다. 표를 그래프로 나타낸다. one-variable linear regression에서 one-variable은 집평수가 된다. 집평수라는 값이 주어지면 집값을 예측하는 regression machine을 만들려고 한다. 제일 먼저 생각해야 할것은 machine learning을 사용해서 풀 수 있는가? 아니면 machine learning을 사용하지 않아도 되는가?이다. 다음 데이터를 보자.
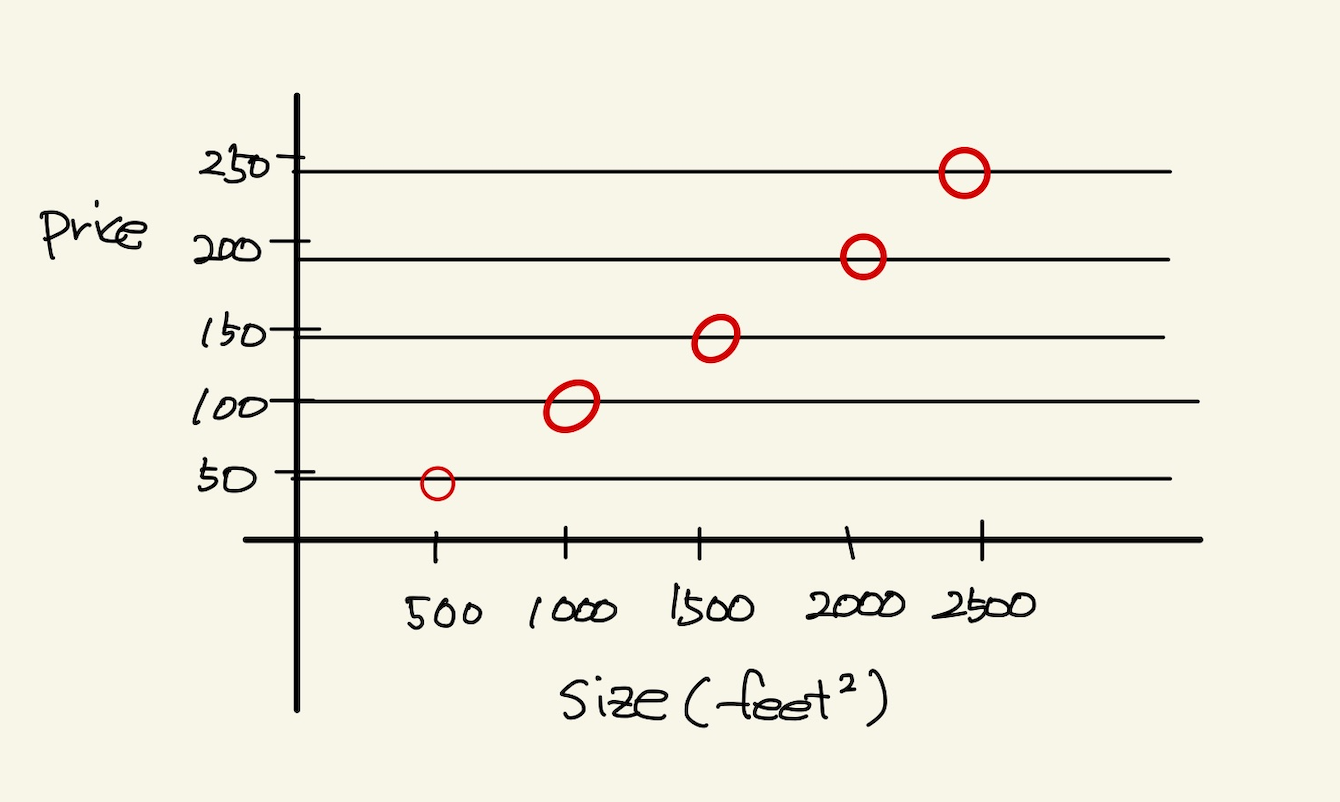
Figure 2: one variable
위와 같은 데이터에선 machine learning을 안 써도 된다. 만일 쓴다면 매우 정확한 machine이 만들어질 것이다.
machine learning의 사용 여부 판단
machine learning이 사용되는 이유는 법칙이나 계산으로 모든 값이 계산이 안되는 경우, 즉 해가 없을때, 가장 가까운 해를 만족시키는 법칙을 찾아내는 것이다. 그런데 위의 식은 y=1/10에 만족한다. 따라서 이 식을 사용하면 된다. machine learning을 굳이 사용하지 않아도 된다. 사용한다면 매우 정확도 높은 machine이 되겠지만…여튼, 만일 이 식을 만족하지 않는 data가 있다면, y=1/10이라는 식을 사용할 수 없고, 그럴 때는 machine learning을 사용해야 한다.
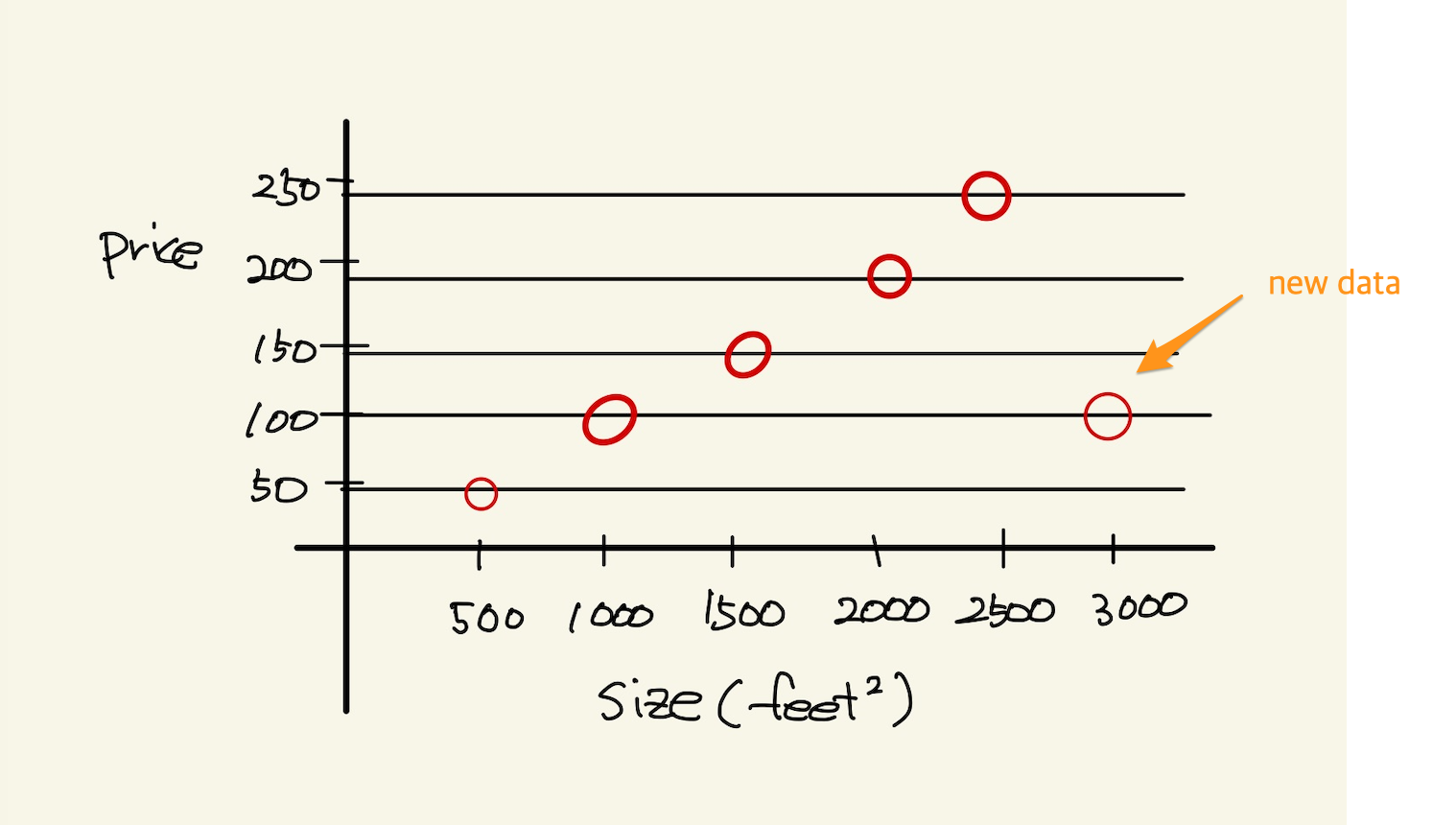
Figure 3: one variable2
machine learning의 사용은 필수
위에서 봤듯이, machine learning을 사용하지 않아도 되는 경우가 있다. 그러나 대부분의 경우, data가 어떤 방정식을 만족하는 경우란 없다. multi feature를 가진 경우에는 더 없게 된다. 따라서 data를 처리해야 하는경우 machine learning을 사용할 수 밖에 없다. 즉 하나라도 예외가 있다면 machine learning을 사용해야 한다.
hypothesis function
machine은 function이라고 했다. machine이 function을 가지고 있다고 생각해도 된다. 그 function을 model 혹은 hypothesis function이라고 부르기로 하자. hypothesis란 이름을 사용하는 이유는 machine이 가진 function이 항상 정답을 도출할수 없기 때문이다. machine learning에서 machine은 애초부터 모든 data에 정답을 도출할 수 없기 때문에, 정답이 아닌 가설이다. 우리의 목표는 data로 이 가설함수를 만드는 것이다. 가설 함수가 가진 parameter를 설정하는 방식이다. hypothesis가 1차방정식이라고 할때, 그 계수는 x가 아닌 \(\theta\) 로 나타낸다. 예를 들면, 아래와 같이 표현한다.
\(h_{\theta}(x) = \theta_{0} + \theta{1}x\)
cost function과 hypotheis parameter update방법
“machine learning"에서 learning을 하는 함수를 cost function, loss function이라고 부른다. 이 함수가 동작해서 hypotheis의 function의 계수를 바꾸게 된다. loss function이 돌아갈려면 우선 machine의 초기 parameter는 임의의 값으로 설정되어 있다고 가정한다. 초기값이 세팅된 machine이 돌아가면, data로 부터 입력을 받고, 입력받은 data로 부터 예측값을 도출한다. 아래 그림처럼 예측값은 식에 따라 나오기 때문에 직선형이다.
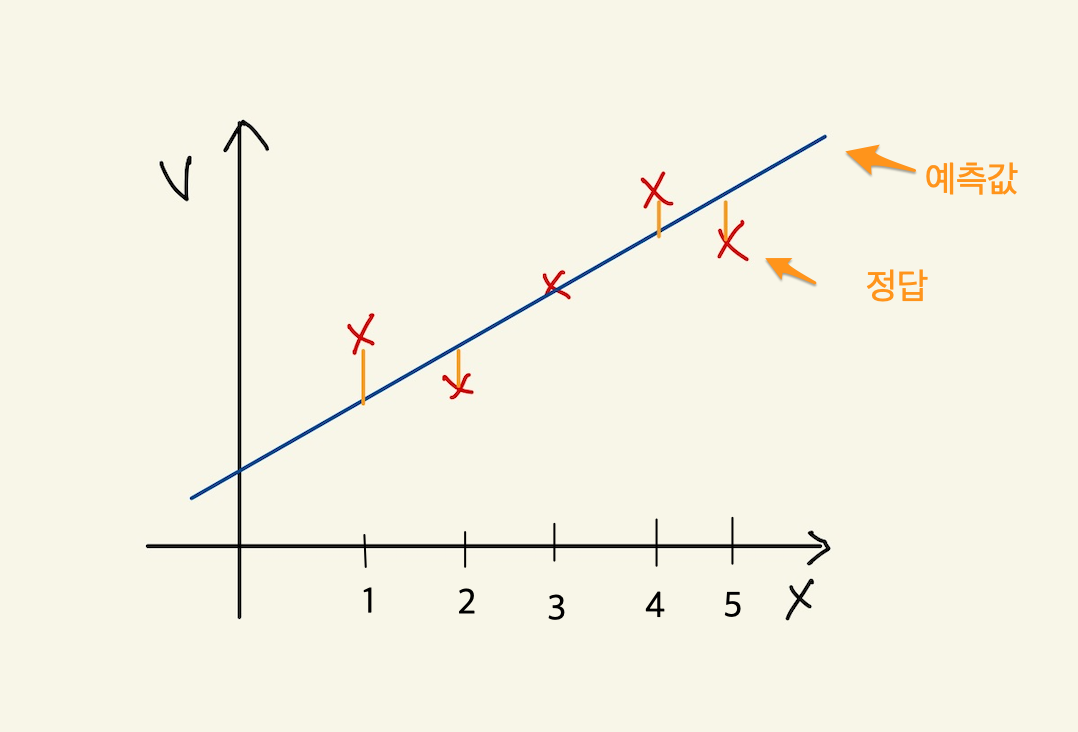
Figure 4: cost function
5개의 data에 대해서 예측값을 뽑아냈다. 이상태에서 예측값과 정답과의 차이를 계산할 수 있다. 그 차이를 loss라고 부른다. 모든 data에 대해서 loss가 발생되고, 여기서는 5개, 그 loss를 모두 더한다. 그리고 평균을 낸다. loss는 예측값-정답인데, 이렇게 하면 그 차이를 제대로 반영하지 못한다. 제곱을해야 한다. 여튼 loss를 모두 더한다. 데이터가 40개 있다면 40개에 대해서 아래와 같은 total loss를 계산할 수 있다. 그리고 평균 loss를 계산할 수 있다.
\(sum of diff=\) \((expectedvalue - datavalue)^{2}\)
\(S=\) \((H(1) - data(1))^{2}\) + \((H(2) - data(2))^{2}\) + \((H(3) - data(3))^{2}\) + \((H(4) - data(4))^{2}\) \((H(5) - data(5))^{2}\)
\(S =\) \(\sum^{n}_{i=1}\) \((H(n)-data(n))^{2}\)
\(loss =\) \(\cfrac{1}{2n}\) \(S\)
10개의 data에 대해서 평균 loss를 구했다면, 위의 그래프에서 예측값과 data에 대한 평균 오차값을 구한것이다. 이제 이값을 가지고 직선을 변경시킨다. 그런데 직선의 계수를 어떤값으로 setting할 것인가? 처음 시작할때는 직선의 기울기와 절편은 임의의값으로 설정했다. 그리고 machine을 돌렸다. 거기로 부터 나온 예측치와 정답의 차를 계산해서 평균 loss를 구했다. 평균 loss를 구해서 model의 parameter를 어떻게 설정하는가? 또 임의로 하자. 이전에 계수와 절편에 따른 방정식이 y=2x+1이였다면, y = 3x+1로 변경했다고 치자. 그러면 다음과 같은 그림이 나온다.
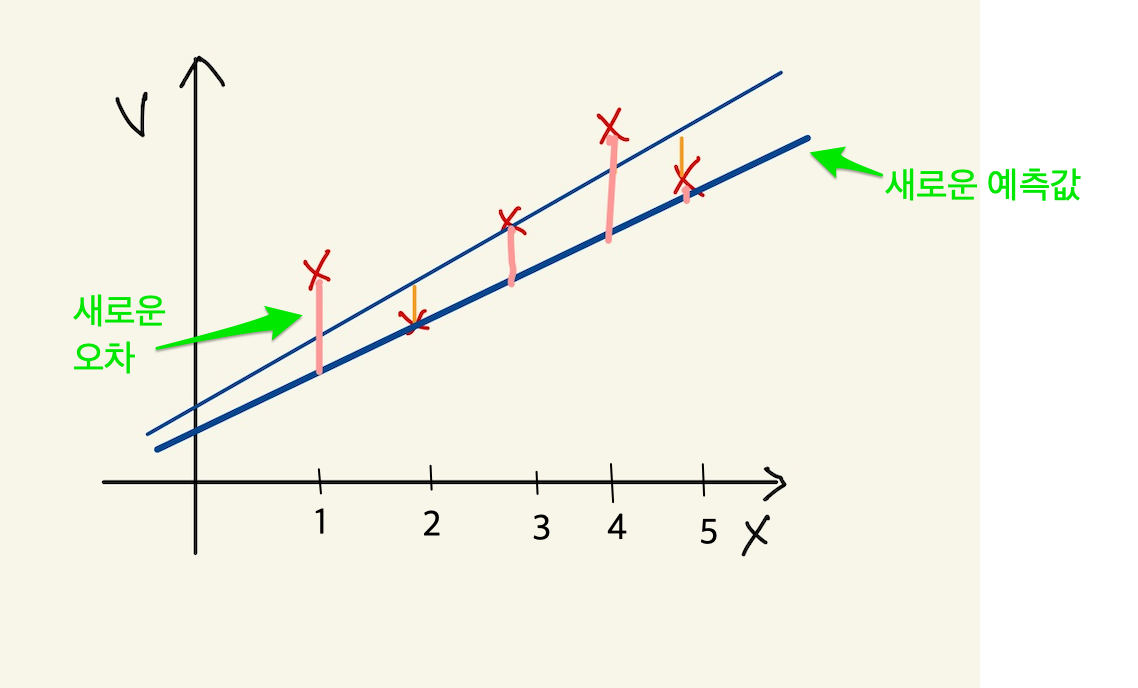
Figure 5: cost function2
여기서 또 예측값과 정답의 차이를 계산한다. 그래서 평균 loss를 구한다. 평균 loss를 구했으니, 다시 직선의 방정식을 정해야 하는데, 이번에는 y =4x+1이라고 하자. 이런 식으로 계속해서 직선을 새로 만들어서 평균 loss의 값을 계속 구한다.
| 직선 | 평균 loss |
|---|---|
| y=2x+1 | 66 |
| y=3x+1 | 45 |
| y=4x+1 | 77 |
| y=5x+1 | 88 |
| ….. | …… |
이것을 그래프로도 만들어보자. 직선의 방정식에서 절편은 1로 고정시켜놓고 기울기만 변화시킨 것이기 때문에 기울기에 대한 평균 loss의 그래프다.
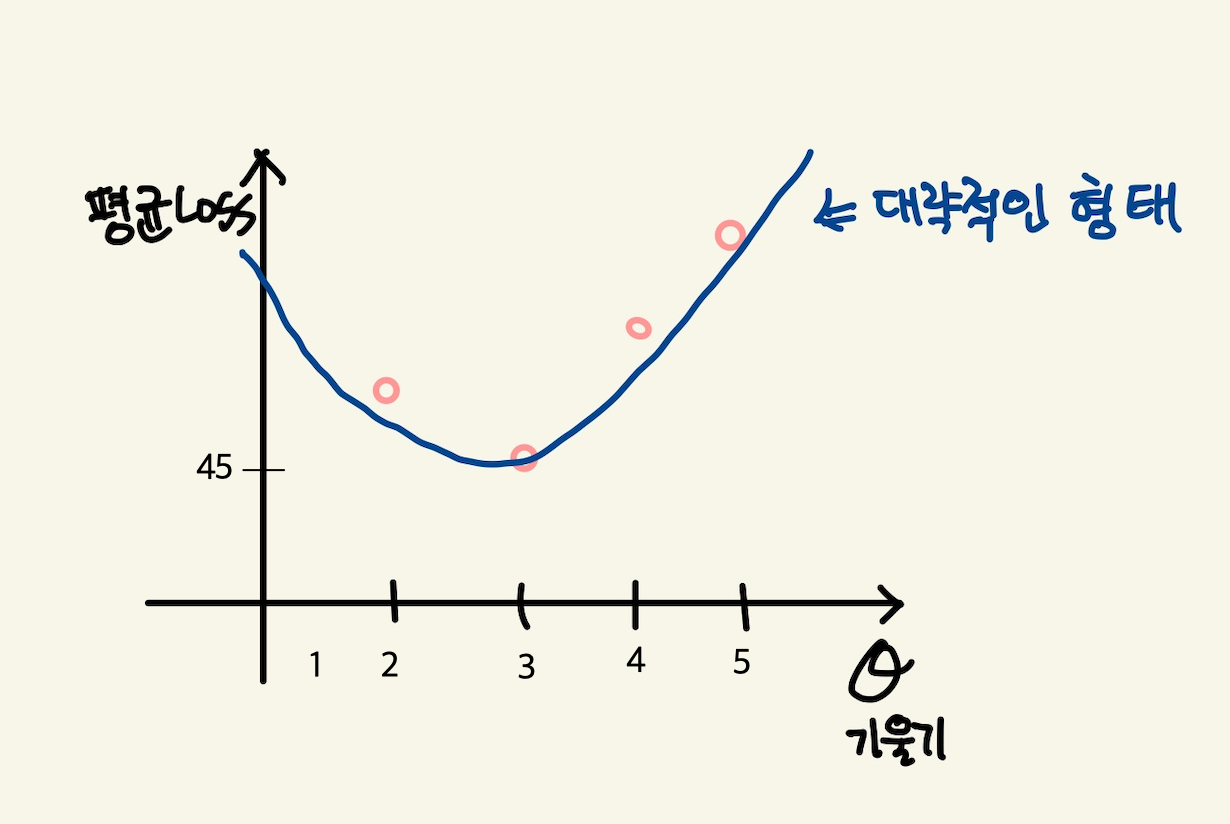
Figure 6: cost function
이렇게 보면 기울기가 3일때 45로 제일 작은 갖는다는 것을 알수 있다. 그리고 앞으로 계속 이렇게 한 다음에 평균 loss가 가장 작을 때 그것이 우리가 구할수 있는 에러를 가장 작게 만드는 직선의 방정식이고 model이 된다. 우리는 training dataset으로 부터 가장 에러가 적은 machine을 만들었다고 봐도 된다. 이 machine으로 test data를 입력해서 예측값을 도출할 수 있는것이다. 하지만, 문제가 있다. 매번 직선의 계수를 우리가 임의로 만들어야 하는가?
cost function과 hypotheis parameter update방법2- 미분의 사용
최소의 loss function을 구하기 위해서 직선을 이리저리 돌려보고 거기서 발생되는 loss의 값이 최소가 될때의 직선을 찾으면 되는데, 직선을 이리저리 돌릴때, 설정하는 계수를 임의의 값으로 해서 loss를 구하는 방법은 비현실적이다. 모든 계수를 입력해본다? 거의 무한대에 해당하는 계수값을 넣어야 한다. 이렇게 하지 않고 다른 방법이 있을까? 우리는 대략 4개의 직선을 만들어서 total loss의 그래프가 2차원이란것을 대략적으로 예측할수 있었다. 그렇다면 기울기에 관한 2차원 함수니까, 미분이 0이되는 값을 찾으면 그때의 기울기값이 최소가되지 않을까?하고 생각할 수 있다.
\(S =\) \(\cfrac{1}{2n}\) \(\sum^{n}_{i=1}\) \((H(\theta_{0}^{n})-data(n))^{2}\)
cost function을 해석하는게 중요하다. 모든 데이터셋의 데이터값과 기울기에 입력되는 parameter값을 모두 대입해서 계산한다고 생각하지 말자. 데이터셋의 모든 데이터가 입력되면 parameter에 관한 방정식이 만들어지고, 이때 기울기값 parameter값을 넣으면 loss가 나온다고 이해하자. 이렇게 이해하는 이유는 cost function이 parameter에대한 함수고, 이를 미분하기 때문이다.
아래 그래프를 보자. 기울기가 3번정도 정해진다면 대략적인 2차함수의 그래프를 알수 있는거 같다. 1번하고 2번했을때는 다양한 2차함수가 나올 수 있다. 근데 3번정도의 기울기값이 있으면 대략적인 2차원 그래프가 정해진다.
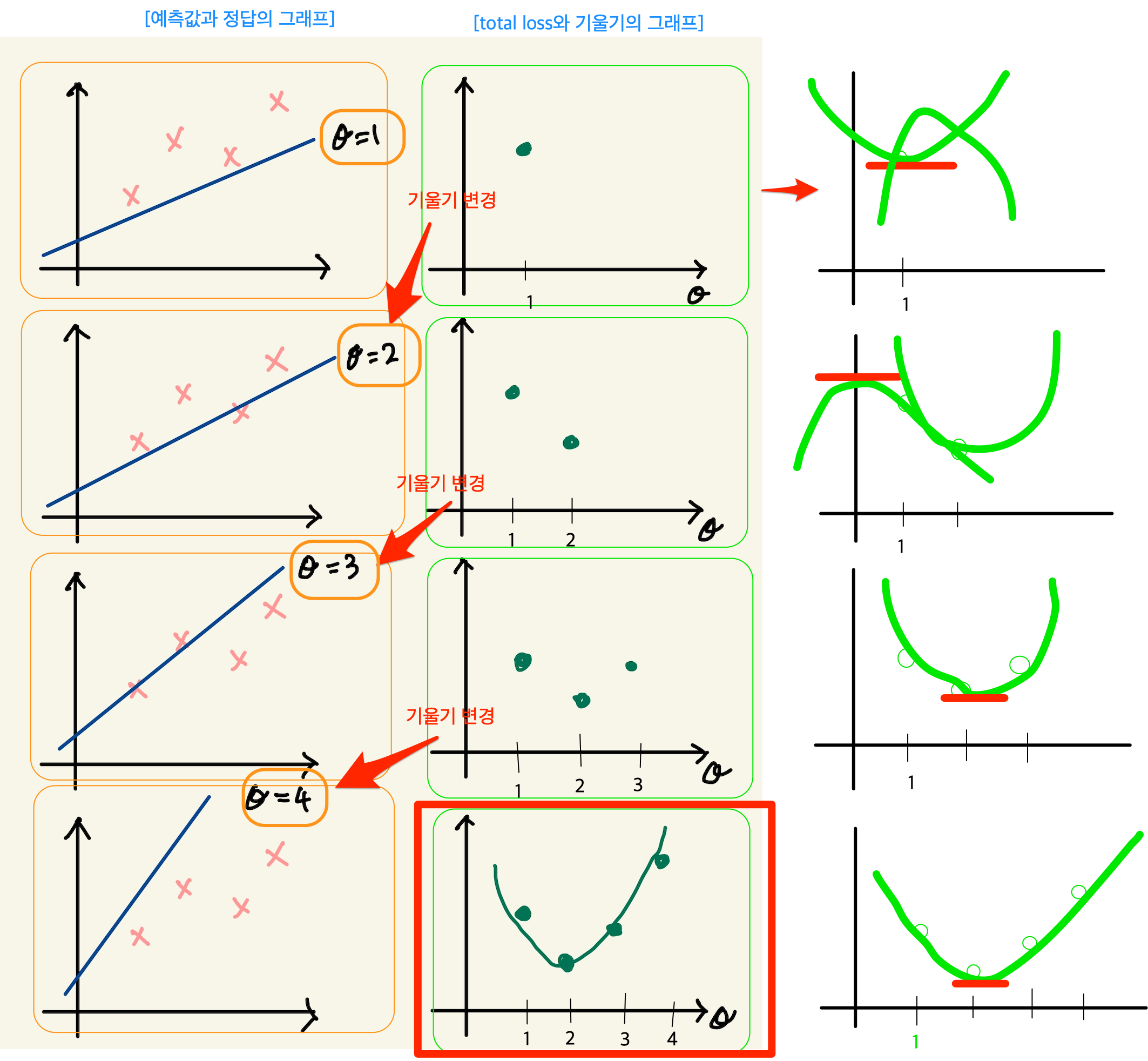
Figure 7: cost function
따라서 loss함수의 2차원 그래프를 가지고 최소값인 기울기를 구할수 있다. 따라서 우리는 그 기울기를 가진 machine이 우리가 찾던 모델이다. 이렇게 해석하면 안된다. 이 설명은 잘 못된 설명이다. 2차원 그래프의 모습은 정해진게 아니기 때문이다. 우리가 2차원 그래프를 위의 loss함수로 그리지만, 거기에 들어가는 계수는 직선의 기울기가 정해진 이후에 2차함수가 설정된다. 따라서 매번 기울기가 정해진 후 2차원 곡선을 그릴 수 있는 것이다. 위의 그림을 보면서 얘기하자면, $θ$가 1일때, 그것에 따른 loss합이 점으로 정해지고 또 다시 기울기를 설정하고 그것에 따라 새로운 loss합이 점으로 그려진다. 점을 이은게 2차함수의 곡선이기 때문에, 계속 그런 식으로 loss함수의 점들을 그려나가서 모이면 2차원 곡선으로 그려진다. 즉 따라서 loss function의 2차원 함수식만 가지고 최종적인 2차원 그래프의 모습을 알수가 없다라고 생각한다. 그래서 2차원식을 미분해서 최소값을 계산으로 구하고 그때의 기울기를 선택하면 안된다. 매번 기울기를 선택하면서 우리는 최소값을 찾아가야한다. 즉 매번 직선의 기울기를 설정하고 설정했을때의 도출된 loss값을 가지고 새로운 직선의 기울기를 조정해야 한다. 그것에 대한 생각을 다음과 같이 정리했다.
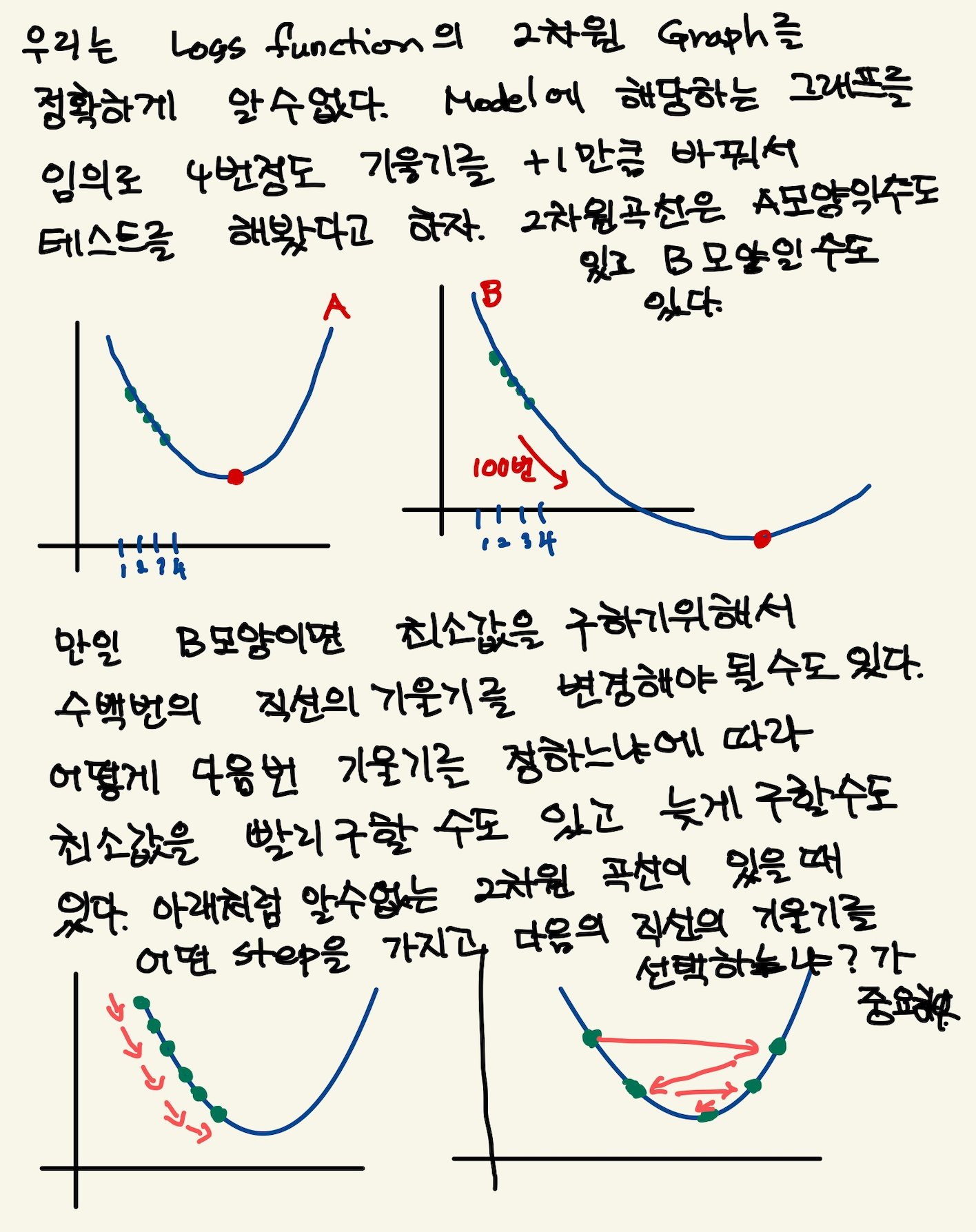
Figure 8: calc5
강사는 설명한다. 직선의 기울기를 선택하고 그 기울기에 해당하는 loss함수의 합을 한점으로 찍고, 또다시 직선의 기울기를 구해서, 그것에 해당하는 loss의 합을 한점으로 찍고 이런 과정을 계속 하다보면, 매번 다른 2차함수 곡선이 그려질 거라는 내 설명과 달리, 강사는 어차피 loss함수의 식인 2차함수 모양으로 그려진다고 한다. 직선의 기울기가 360도 회전하는 그 모든 값에 loss함수가 2차곡선으로 정해져 있다고 한다. 다만 단순한 2차곡선의 경우는 미분이 0인값 계산이 가능하지만, 복잡한 경우에는 예를 들어, 2차곡선이 아닌 100차곡선에서 기울기가 0인점을 사용할 수 없기 때문에 경사하강법을 쓴다고 말한다. 경사하강법은 최소값을 찾아나가는 방법이다. 나는 애시당초 loss function에서 미분값이 0이되는 값은 구해도 쓸모가 없기때문에, 즉 매번 기울기가 바뀌니까, 경사하강법으로 최소값을 찾아야 한다는 입장이고, 강사는 계산의 복잡함으로 인해 미분값이 0이 되는 최소값은 구하기 힘들다는 것이다. 따라서 경사하강법을 써야 한다는 건데, 누구 말이 맞던간에 결론은 경사하강법이다.
경사하강법
미분으로 최소값을 구하는 방법이 아닌, 강사가 비유한 것처럼, 산에서 내려올때, 그 지점에서 올라가야할 지 내려가야할 지 미분으로 방향을 찾고 그 방향으로 부터 얼마나 이동할 지는 현재의 기울기에서 learning rate와 미분값으로 곱해진 값을 빼는 식으로 계산한다. 여튼 이런식으로 최소값을 찾아나가는 방식이 gradient descent 방식이다.
local minima
최소값을 찾아서 후래시로 한단계 한단계 나가는 방식은 local minima 문제가 있을수 있다. 즉 계속 기울기를 조정해 나가면서 최소값을 찾았다고 생각하지만, 최소값이 여러개가 있을 수 있기 때문이다.
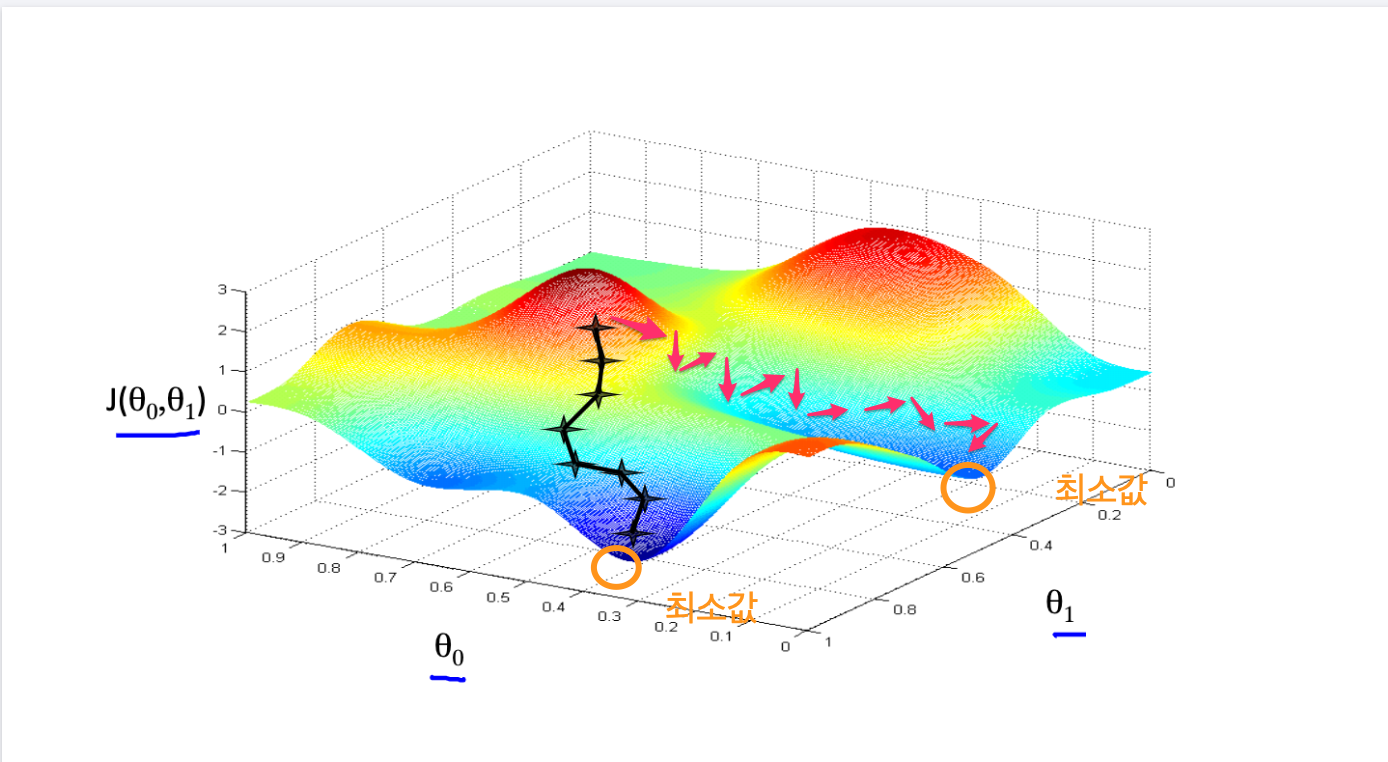
Figure 9: local minima
global minima가 1개만 있는 경우도 있다. 이런경우 graph모양이 convex형태일 경우가 많다.
미분값에 대해서
일단 machine이 초기값을 가지고 동작이 시작되었다고 하자. 초기값이란 직선의 기울기가 임의로 주어졌다는 것이다. 그러면 예측값을 구할 수 있고, 정답은 data로 부터 주어진다. 그렇다면 loss function으로 부터 loss의 총합을 구할수 있다.
\(S =\) \(\sum^{n}_{i=1}\) \((H(n)-data(n))^{2}\)
즉 모든 data를 hypothesis function에 넣어 예측값을 구하고 data에서 정답을 빼서 total loss의 합을 구할수 있다. 이것은 2차함수로 표현되는 loss function의 한점이라고 했다. 그런데 여기서는 처음 machine을 만들때 임의의 기울기값이 입력이 되었기 때문에 loss function이 계산이되어 일종의 상수값인 loss들의 합이 나온다. 즉 total loss값이 나오는데, 이것은 우리가 원하는 미분값과는 관련이 없다. 우리는 초기 기울기값이 입력이 되지 않은 변수 형태의 loss function식을 사용해야만, 기울기에 관한 2차방정식과 미분 방정식을 얻는다. 그런데 가만보면, loss function의 식이 좀 특이하다. 그냥 2차함수가 아니다. 모든 데이터에 대해서 예측값과 정답의 차이를 더해서 만든다. 엄청나게 많은 계산량이 예상된다. 여튼 모든 data에 대해 처리하기 때문에 식에 sigma를 사용하는것이다. 그리고 그렇게 만들어진 loss function에 미분을 취하면 경사하강법에 쓰이는 미분식이 나온다. 예를 들어보자.
| x | y |
|---|---|
| 3 | 10 |
| 4 | 13 |
| 5 | 17 |
\(h(\theta) = \theta_{0} x\)
\(J(\theta_{0})\) = \(\sum^{n}_{i=1}\) \((H(n)-data(n))^{2}\)
위와같은 데이터가 있다면 loss function은 다음과 같이 계산될 수 있다. 모든 데이터에 대해서 다 더하기때문에 계산량이 만만치 않다. 여튼 이것을 다 계산해야 2차함수가 나오는 것이다. 그리고 이 loss function에 미분을 해야 미분식이 나온다.
\(J(\theta_{0}) =\) \((3\theta - 10)^{2} +\) \((4\theta - 13)^{2} +\) \((5\theta - 17)^{2}\)
1변수 경사하강법 예시
임의의 machine을 만들었다고 하자. 기울기를 4로 하는 직선 model을 가진 machine을 실행시켜서 얻은 그래프가 다음과 같다고 하자. 초기값은 4일때, machine의 예측값과 정답이 보인다.
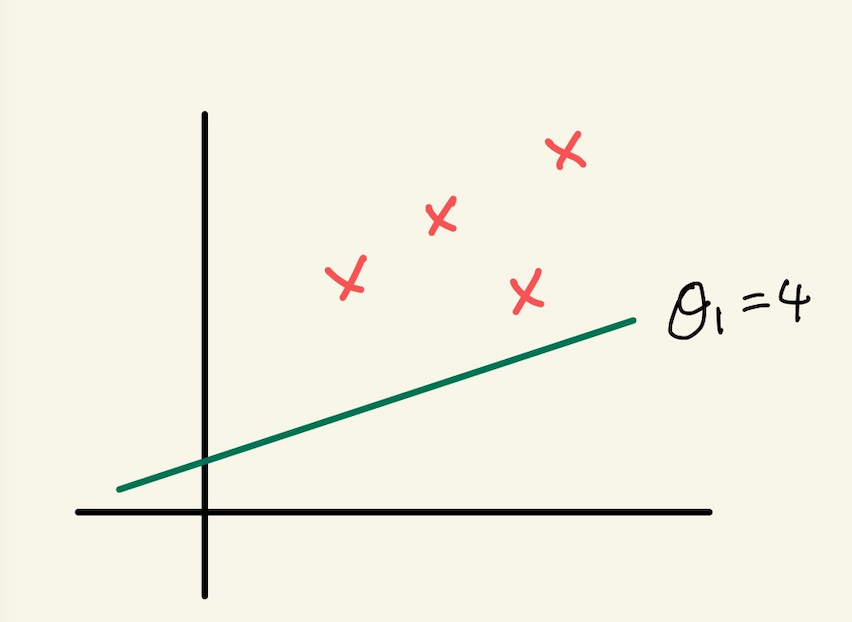
Figure 10: gd1
경사하강법이란 기울기를 업데이트 하는 식이다. 즉 learning의 핵심이다. 새로운 기울기는 기존의 기울기 - learning rate*미분값으로 계산된다. 여기서 중요한게 미분값인데, 이 미분값은 loss function으로 부터 구해진다.
여튼 loss function은 이미 주어졌다고 하자. 우리가 원하는 것은 어떻게 기울기를 update하느냐에 관심이 있기 때문에, loss function이 주어지는 것이다. loss function을 미분하고 이값이 어떻게 기울기에 영향을 미치는가에 관심이 있다.
loss function = \(2\theta_{1}^{2} -4\theta_{1} +5\) = \(2(\theta_{1}-1)^{2}\) \(+3\)
위의 model에서 data의 정답과 예측값의 차이를 모두 더한값을 graph에 나타내면 한점으로 표시할 수 있는데, 이 점은 loss function으로 나타내지는 graph에서의 한점이다. 이걸 그림으로 표현하면 다음과 같다.
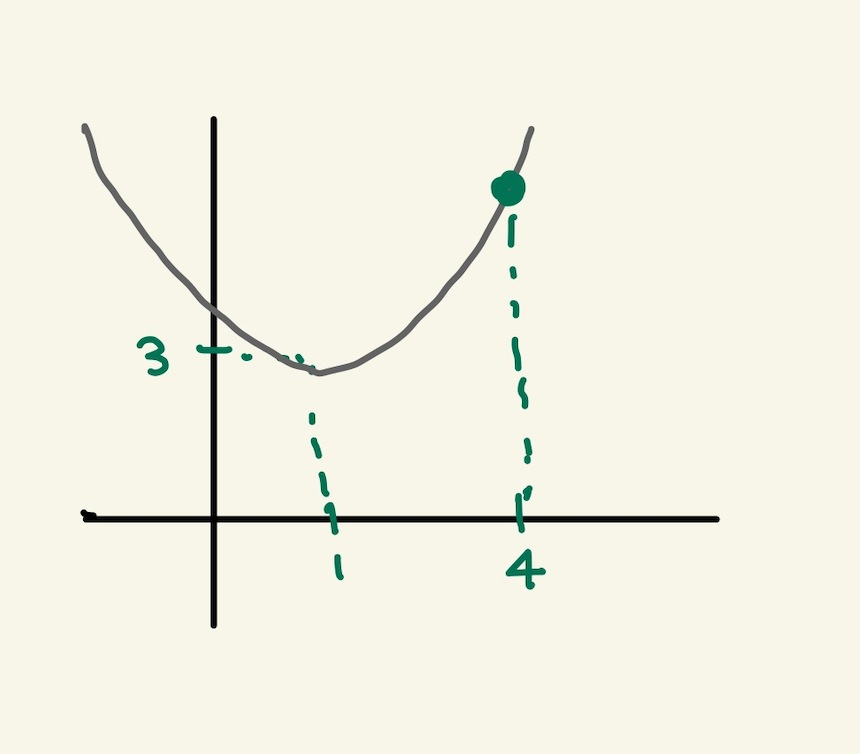
Figure 11: gd2
여기서 후래시를 비춰본다는 표현을 쓰는데, 왼쪽으로 갈지 오른쪽으로 갈지 방향을 구해야한다. 어떻게 구하는가?
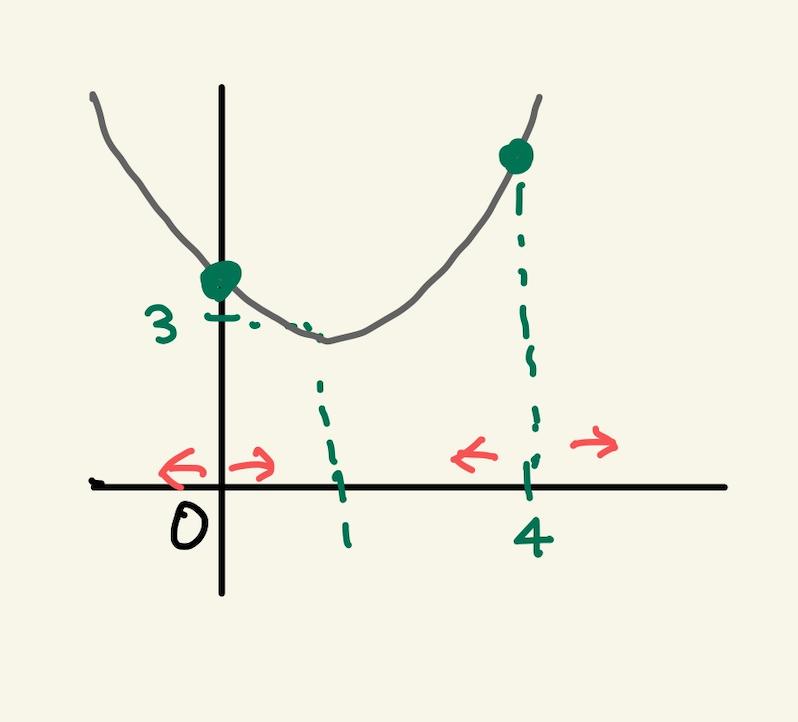
Figure 12: gd3
방향을 구할때 loss function의 미분을 사용한다. 미분값이 음수냐, 양수냐에 따라서 방향이 정해진다. 미분을 해보자.
loss function = \(2\theta_{1}^{2} -4\theta_{1} +5\)
미분값: \(4\theta_{1}-4\)
그러면 기울기가 4일때는 12라는 양수값이 나온다. 참고로 기울기가 0일때의 값도 구하면 -4라는 값이 나온다. 그러면 여기서 4일때는 어떤식을 통해서 더 낮은곳인 왼쪽으로 가고, 0일 경우 어떤 식을 통해서 더 낮은 곳인 오른쪽으로 이동하게 하고 싶다. 그 어떤 식은 다음과 같다. 여기서 $α$는 step size다. 그리고 그 값은 0.1로 하자.
새로운 기울기 = 원래의 기울기 - \(\alpha\) x 미분값
이 식에 맞추어 계산해보자. 기울기가 4일때 새로운 기울기는 4 - 0.1(12) = 2.8 이 나온다. 즉, 왼쪽으로 이동하게 된다. 기울기가 0일때도 계산해보자. 기울기가 0일때, 새로운 기울기는 0 -0.1(-4) =0.4 값이 나와서 오른쪽으로 이동하게 된다. 그런데 step size는 동일하지만, 이동거리는 차이가 있다. 4일때는 1.2만큼 왼쪽으로 이동했다면, 0일때는 0.4만 오른쪽으로 이동했다. 왜 같은 거리만큼 이동하지 않았을까? 기울기의 크기가 크다면 경사가 가파르다는것을 의미한다. 반면 0일때의 기울기는 좀더 경사가 완만한것이다. 완만하다는건 최소점에 가까워졌다는 것을 의미한다. 그래서 이동거리가 짧은것이다. 물론 이것이 꼭 옳은 것만은 아니다. 다음의 경우를 보자.
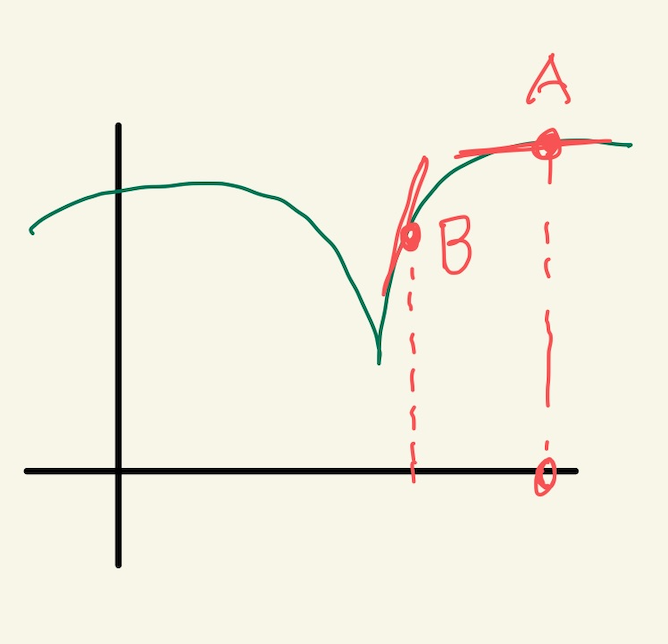
Figure 13: gd4
위의 경우 B의 경우 경사가 급하다. 그런데 최소점과 더 가깝다. A는 최소점과 거리가 멀지만 완만하다. 이런경우 경사가 급해서 이동거리가 길게 되면 최소점을 지나게 된다. 또한 완만한점에서는 이동거리가 작아져서 최소점에 수렴속도가 느려지게 된다. 즉 위에서 새로운 기울기를 구하는 식은 이 경우에는 맞지 않는다. 다른방법을 사용해야 한다.
아까 과정을 이어서 설명하면, 기울기가 4일 때 새로운 기울기는 2.8로 구했다. 이제 2.8의 기울기를 가진 모델에서 예측값과 정답사이를 계산해서 다시 점을 찍으면 2차곡선인 loss function의 점이 된다. 여기서 다시 미분값과 새로운 기울기를 구하는 식을 계산해서 새로운기울기를 만든다. 계속 이과정을 반복한다. 이 과정을 계속하면 최소점에서 거의 멈추게 된다. 넘어가지 않는다. 그 이유는 기울기를 사용하기 때문이다. 0에 가까운 기울기에서 새로운 기울기를 구해도 0과 가까울 뿐이다.
지금까지 경사하강법을 요약하면, 기울기를 사용해서 모든 data에 대해 예측한 값과 정답간의 차이를 합한값을 구하고 기울기를 다시 설정해서 예측값과 정답의 차이를 합한값을 구하고 이과정을 계속 반복해서 최소의 예측값과 정답간의 차이를 구하는 것이 아니였다. 이게 좀 예상밖인데, 경사하강법은 예측값과 정답의 차이를 계산할 필요가 없다. 경사하강법은 model의 parameter를 수정하기 위해서 loss function의 미분값과 learning rate를 계산을 반복할 뿐이다. loss function의 값을 사용하지 않는다는 것이다. 기울기의 미분값과 learning rate를 계산해서 새로운 기울기를 만들고, 만든 기울기의 미분값과 learning rate를 계산해서 새로운 기울기를 계속 만들어낸다. 언제까지? 기울기, 즉 model의 parameter가 변화가 없을때까지…
2변수 경사하강법 예시
변수가 2개인 경우를 알아보자. 이 경우 model은 y=ax +b꼴일수도 있고, y=ax^2+b꼴일수도 있다. 여튼 우리가 관심있는 것은 loss function이기 때문에 loss function이 다음과 같다고 하자.
\(J(\theta_{0},\theta_{1})=\) \(\theta_{0}^{2}+3\theta_{1}^{2}\) \(-2\theta_{0}\theta_{1}\) \(+ 4\theta_{0} -5\theta_{1}\) \(+3\)
\((\theta_{0}=-1, \theta_{1}=2)\) 일때를 생각해보자. 이런 기울기를 가질때, loss function의 값은 다음과 같다. 1+12-2(-1x2)+4(-1)-5(2)+3 = -20의 값을 갖는다. loss function의 미분값을 통해서 방향과 step size를 통해서 최소점을 찾아간다. 그럴려면 미분을 해야하는데, 2개의 변수가 있기 때문에 편미분을 해야 한다. 편미분을 해보자. 그리고 \((\theta_{0}=-1, \theta_{1}=2)\) 일때 미분값을 구하면 다음과 같다.
\(\cfrac{dJ}{d\theta_{0}}\) \(=2\theta_{0}\) \(-2\theta_{1}\) \(+4\) \(=2(-1) -2(2) +4\) \(= -2\)
\(\cfrac{dJ}{d\theta_{1}}\) \(= 6\theta_{1}\) \(-2\theta_{0}\) \(-5\) \(=6(2) -2(-1) -5\) \(=9\)
이제 새로운 기울기를 구해보자. learning rates를 0.1이라고 하자. 그러면 공식에 의해서 새로운 기울기는 다음과 같다.
새로운 기울기 = 옛날 기울기 - \(\alpha\) x 미분값
\(\theta_{0}\) = \(-1\) \(- 0.1\) x \((-2)\) \(= -0.8\)
\(\theta_{1}\) \(= 2 - 0.1\) x \(9\) \(= 1.1\)
이것을 model의 새로운 기울기로 설정한다. 그리고 새로운 기울기의 미분값을 구하고 learnin rate와 계산해서 새로운 기울기를 구하고, 또 미분값과 learning rate를 이용해서 또 다시 새로운 기울기를 얻는 과정을 계속한다.
요약하면, 변수가 1개인 경사하강법과 변수가 2개인 경사하강법은 거의 동일하다. 다만 변수가 2개이기 때문에 편미분을 통해서 각각의 새로운 기울기를 구한다. 새로 구해진 기울기에서 미분값과 learning rates를 사용해서 새로운 기울기를 구하고, 다시 그 기울기의 미분값과 learning rate를 계산해서 새로운 기울기를 구한다.
그리고, 예측값과 정답의 차이를 매번 계산하지 않고 필요없는 식으로 묘사했지만, 예측값과 정답의 차이를 나타내는 식은 machine이 돌아가기전에 구해져 있어야 한다. 왜냐면 미분식은 정답과 예측값의 차의 제곱으로 나타내지기 때문이다. 매번 machine이 돌아가면서 그 loss값을 계산하지 않지만, 처음 machine이 만들어질때는 미분식은 존재해야 한다. 그래야만, machine이 매 epoch마다 기울기를 수정할때 미분값을 사용할 수 있기 때문이다.
