[machine learning] day17-multiple-variable-regression
이번 강의의 특징
이번 강의의 순서는 좀 뒤죽박죽이다. 알아서 정리하기로 한다.
Multiple Variable data
다음과 같은 여러개의 집에 관한 여러 feature가 있는 data가 있다고 하자. 여기서 price를 예측하는 machine learning을 만들려고 한다. 따라서 price가 정답인 training dataset으로 보면 된다.
| size | number of bedrooms | number of floors | Age of home | Price |
|---|---|---|---|---|
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
machine을 만들자.
machine은 hypotheis function, 즉 model을 만드는 일이다. model은 각 feature를 linear하게 더한 식으로 만들 수 있다.
\(H(\theta)=\) \(\theta_{0}\) \(+ \theta_{1}x_{1}\) \(+ \theta_{2}x_{2}\) \(+ \theta_{3}x_{3}\) \(+ \theta_{4}x_{4}\)
machine의 초기값은 임의의 값으로 주기로 한다.
\(H(\theta)=\) \(80\) \(+ 0.1x_{1}\) \(+ 0.01x_{2}\) \(+ 3x_{3}\) \(-2x_{4}\)
machine에 행렬도입
이렇게 하면 machine을 만든 것이다. 그런데 multi variable data를 가지고 만드는 machine은 좀 다르다. model을 행렬로 나타낸다. model이 function이 아닌 matrix나 vector로 나타내 진다. matrix나 vector도 모두 function이였음을 기억하자. 예를 들어서,
\(\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}\)
위와 같은 vector는 1차원의 입력을 받아서 3차원의 공간에 mapping하는 함수다.
\(\begin{bmatrix} 1 & 1 & 0 \\ 1 & 0 & 1 \end{bmatrix}\)
위와 같은 matrix는 3차원의 입력을 받아서 2차원 공간에 mapping하는 함수다.
machine의 hypothesis function을 다시 쓰면 다음과 같다.
\(H(\theta)=\) \(\theta_{0}\) \(+ \theta_{1}x_{1}\) \(+ \theta_{2}x_{2}\) \(+ \theta_{3}x_{3}\) \(+ \theta_{4}x_{4}\)
\(H(\theta)=\) \(\begin{bmatrix} \theta_{0} \\ \theta_{1} \\ \theta_{2} \\ \theta_{3} \\ \theta_{4} \end{bmatrix}^{T}\) \(\begin{bmatrix} x_{0} \\ x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix}\)
feature 4개이지만, 절편에 해당하는 dummy값을 추가한다. \(x_{0}\) 값은 실제 있는 데이터가 아니기 때문에 1로 설정한다.
Multi-variable regression Gradient Descent
multi-variable regression은 여러개의 feature를 가진 데이터를 처리한다. machine도 여러개의 feature를 처리하기위해서 행렬을 사용하게 된다. 그러나 multi-variable regression에서 gradient descent는 행렬을 사용해서 계산하는건 배우지 않는다. 1차 함수식으로 생각하고 계산한다. Gradient descent는 learning의 핵심이다. 즉 새로운 기울기를 구하는 것이다. 일종의 법칙인 새로운 기울기는 예전기울기 - learning rate*미분값이라는 식이 쓰인다. 이 식을 계산하기 위해선 미분값을 구해야 하는데, 미분값은 loss function을 구해야 한다. loss function을 구하기 위해선 hypothesis function을 알아야 한다. 그리고 hypothesis function을 알기 위해선 data가 있어야 한다. 이것을 순차적으로 진행해 보자.
data
다음과 같은 data가 있다고 하자.
| X1 | X2 | Y |
|---|---|---|
| 1 | 2 | 5 |
| 3 | -1 | 7 |
| 2 | 3 | 4 |
hypothesis function
machine의 model이 다음과 같다. multi variable regression처럼 feature가 많으면 machine의 model은 matrix로 나타낼수 있다고 했다. 하지만, 여기선 행렬로 표현하지 않기로 한다.
\(H =\) \(\theta_{0}\) \(+ \theta_{1}x_{1}\) \(+ \theta_{2}x_{2}\)
loss function
loss function을 구해보자. loss function은 hypotheis function을 사용한다.loss function은 모든 data를 입력해서 얻어지는 식이다. 위에는 3개의 data밖에 없기 때문에, 3개의 data를 입력해서 식을 구하지만, 100개 있다면 100개의 data를 입력해서 계산해야 한다.
\(J(\theta_{0},\theta_{1},\theta_{2})\) \(=\cfrac{1}{2*3}\) \((\theta_{0}\) \(+ \theta_{1}*1\) \(+ \theta_{2}*2 -5)^{2}\) + \((\theta_{0}\) \(+ \theta_{1}*3\) \(+ \theta_{2}*(-1) -7)^{2}\) + \((\theta_{0}\) \(+ \theta_{1}*2\) \(+ \theta_{2}*(3) -4)^{2}\)
미분식
위에 구한 loss function에 대한 미분식을 구한다. 미분식은 편미분으로 구한다.
\(\cfrac{dJ(\theta_{0},\theta_{1},\theta_{2})}{d\theta_{0}}\) \(=\cfrac{1}{3}\) \((\theta_{0}\) \(+ \theta_{1}*1\) \(+ \theta_{2}*2 -5)*1}\) \(+\) \((\theta_{0}\) \(+ \theta_{1}*3\) \(+ \theta_{2}*(-1) -7)*1\) + \((\theta_{0}\) \(+ \theta_{1}*2\) \(+ \theta_{2}*(3) -4)*1\)
\(\cfrac{dJ(\theta_{0},\theta_{1},\theta_{2})}{d\theta_{1}}\) \(=\cfrac{1}{3}\) \((\theta_{0}\) \(+ \theta_{1}*1\) \(+ \theta_{2}*2 -5)*1}\) \(+\) \((\theta_{0}\) \(+ \theta_{1}*3\) \(+ \theta_{2}*(-1) -7)*3\) + \((\theta_{0}\) \(+ \theta_{1}*2\) \(+ \theta_{2}*(3) -4)*2\)
\(\cfrac{dJ(\theta_{0},\theta_{1},\theta_{2})}{d\theta_{2}}\) \(=\cfrac{1}{3}\) \((\theta_{0}\) \(+ \theta_{1}*1\) \(+ \theta_{2}*2 -5)*2}\) \(+\) \((\theta_{0}\) \(+ \theta_{1}*3\) \(+ \theta_{2}*(-1) -7)*(-1)\) + \((\theta_{0}\) \(+ \theta_{1}*2\) \(+ \theta_{2}*(3) -4)*3\)
경사하강법
이렇게 미분식까지 구했단면 실질적 learning에 해당하는 경사하강법을 구할 준비가 다 됐다. 경사하강법의 식은 다음과 같다.
새로운 기울기 = 지금 기울기 - \(\alpha\) * 미분값
이렇게 구하면 된다. 그런데 기울기가 여러개이기 때문에 여러개에 대해서 각각 저렇게 구해주면 된다.
Polynomial variable linear regression
machine의 model이 1차함수만 되라는 법은 없다. one-variable, multi-variable의 형태가 아닌경우도 가능하다. 아래 예를 들었다.
\(H=\) \(\theta_{0} +\) \(\theta_{1}x_{1}^{2} +\) \(\theta_{2}x_{2}\)
\(H=\) \(\theta_{0} +\) \(\theta_{1}x_{1}^{2} +\) \(\theta_{2} \sqrt{x_{2}}\)
그럼 언제 위와같은 model을 사용하는가? feature space에 따라 선정한다.
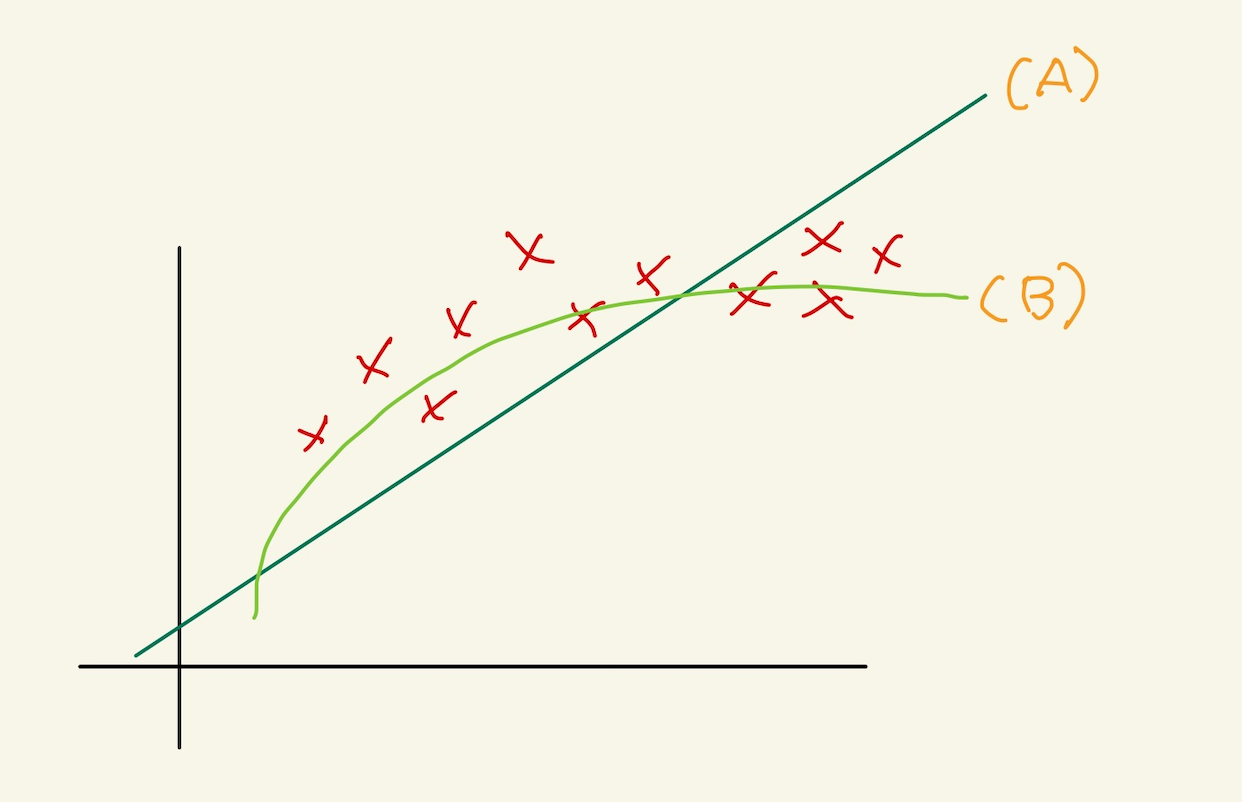
Figure 1: poly1
위의 data의 분포도에 A같은 model을 사용할 경우 에러가 많이 날것이란걸 알수 있다. 반면에 B와 같은 모델은 에러가 적을것이라 충분히 예상할 수 있다. B와 같은 모델을 사용하려면, hypothesis function에서 square를 사용한다면 증가율을 완만히 해서 비슷한 모양의 모델을 만들수 있다.
feature space에 따른 모델
데이터가 다음과 같이 주어졌다고 하자.
| X | Y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 6 |
그리고 feature space를 보니 다음과 같은 모양이다.
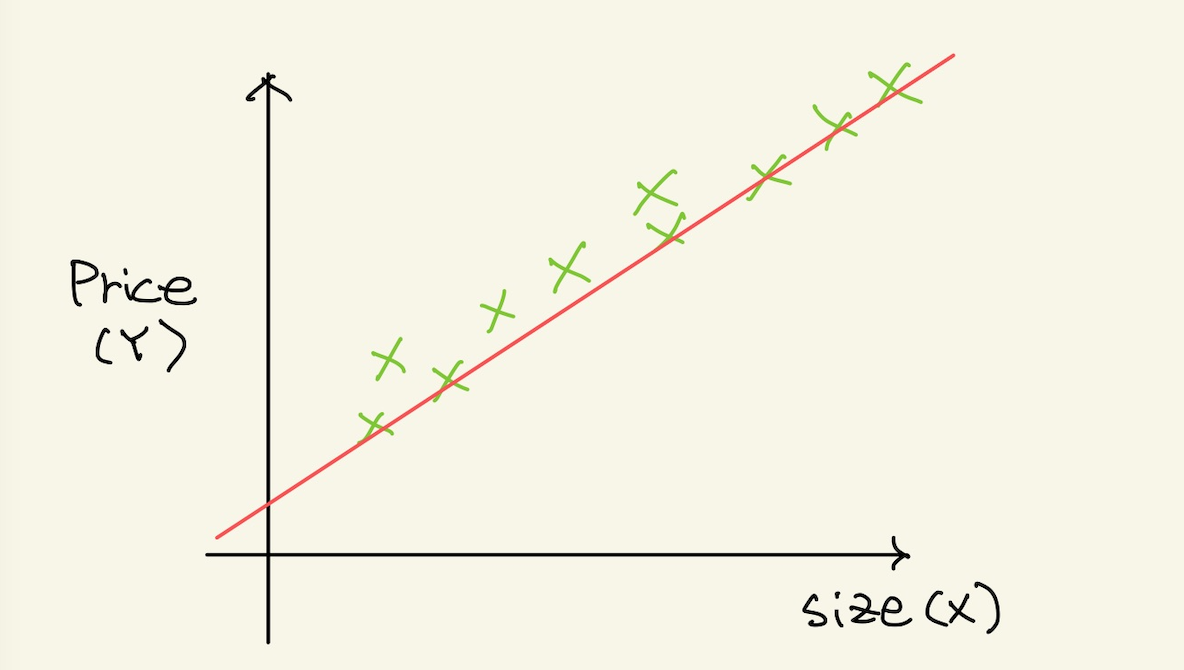
Figure 2: poly2
이런경우 hypotheis는 one-variable이나 multi-variable과 그닥 다르지 않다.
\(H =\) \(\theta_{0}\) + \(\theta_{1}x_{1}\)
그런데 다음과 같은 feature space를 보자.
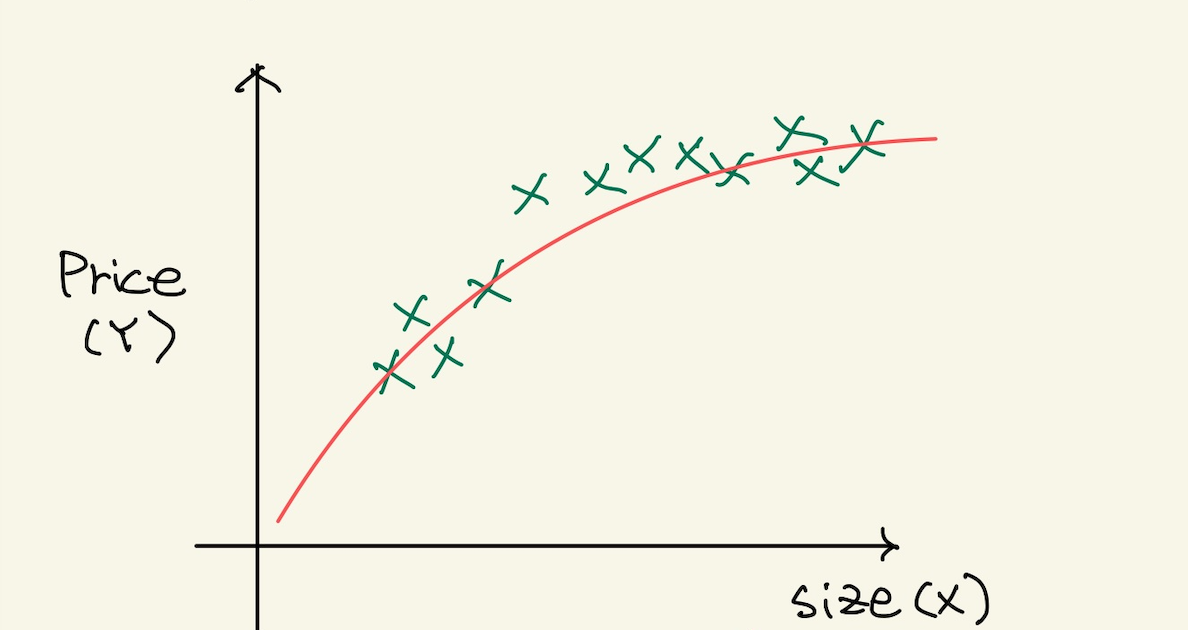
Figure 3: poly3
data가 끝으로 갈수록 크기가 완만해진다. 이것을 수식으로 처리 하기 위해서 제곱근값을 feature로 추가하는 방법을 쓴다.
| X | \(\sqrt{X}\) | Y |
|---|---|---|
| 1 | 1 | 3 |
| 2 | \(\sqrt{2}\) | 5 |
| 3 | \(\sqrt{3}\) | 6 |
hypotheis function도 다음과 같이 바뀐다.
\(H =\) \(\theta_{0}\) + \(\theta_{1}x_{1}\) + \(\theta_{2}\sqrt{x_{1}}\)
여기서 중요한것은 새로 추가되는 feature는 제곱근의 값인데, 제곱근은 $x1$의 값을 가지고 제곱근을 만든다는 것이다. data 자체를 새롭게 만들수는 없기 때문에, 기존의 x값을 이용해서 만들어내는 자료기 때문이다.
또 다른 예를 보자.
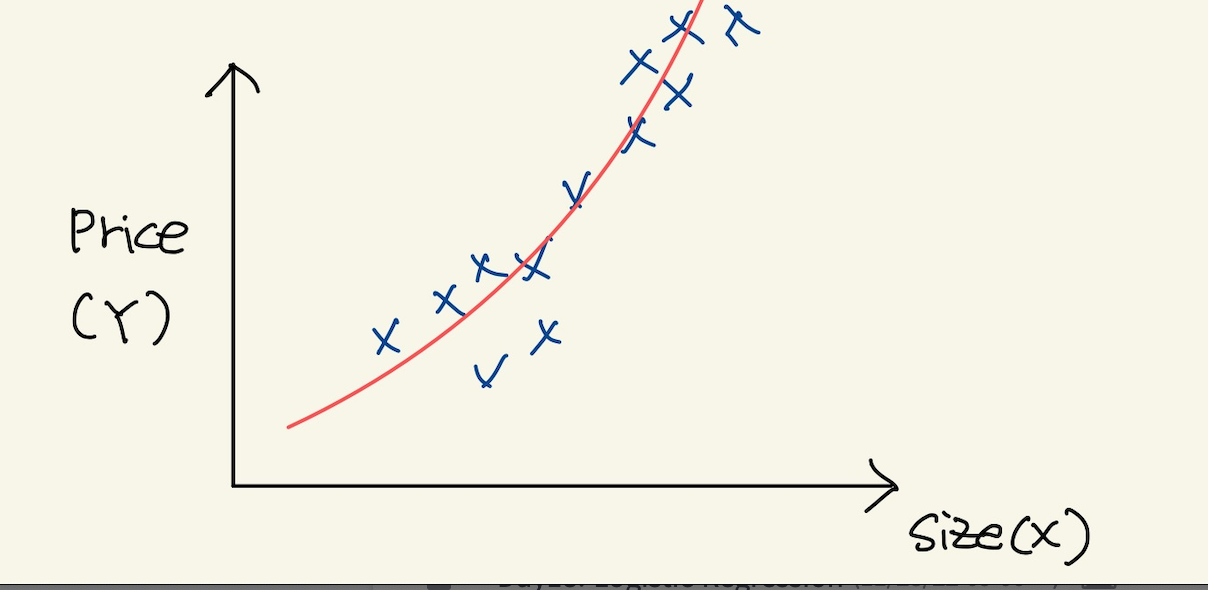
Figure 4: poly4
이 경우에, 끝으로 갈수록 값이 증가한다. 이런경우는 제곱을 feature로 추가 한다. 없는 feature를 추가한다.
| X | \(X^{2}\) | Y |
|---|---|---|
| 1 | 1 | 3 |
| 2 | 4 | 5 |
| 3 | 9 | 6 |
hypotheis function도 다음과 같이 바뀐다.
\(H =\) \(\theta_{0}\) + \(\theta_{1}x_{1}\) + \(\theta_{2}x_{1}^{2}\)
여기서도 새로운 feature인 제곱은 기존에 있던 x의 값을 제곱한 것이다.
feature space와 and feature scaling
multi variable feature를 사용하면, one-variable보다 많은 feature가 사용된다. 여러개의 feature를 사용하는 machine learning에서 고려되어야 할 것들이 생기는데, 그게 feature scaling이다. feature scaling을 얘기하기 위해서는 feature space와 decision boundary라는 개념도 알아둘 필요가 있다.
feature space
입력이 될 data를 graph로 나타낼 수 있는데, feature를 축으로 하는 공간에서 data를 표시한다. 예를 들어보자.
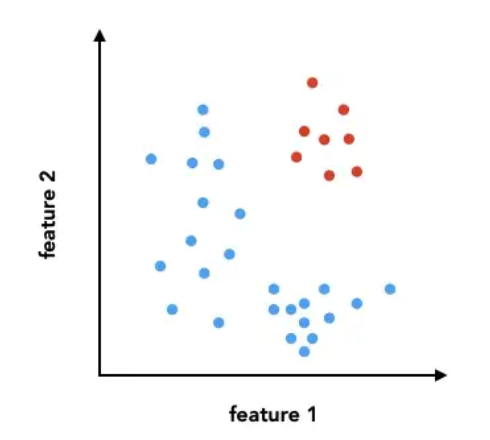
Figure 5: feature space1
feature가 2개면 2차원 공간이 생기고 거기에 data가 표시된다. 우리 데이터의 경우 dummy까지 포함해서 5개의 feature가 있기 때문에 5차원 feature space가 생기게 된다. 여기게 생각해 볼것은 feature space라는게 data를 공간으로 나타낸것이고, data는 machine의 입력이 된다. machine이 matrix를 사용하게 된다면, matrix의 입력공간이 feature space가 된다.
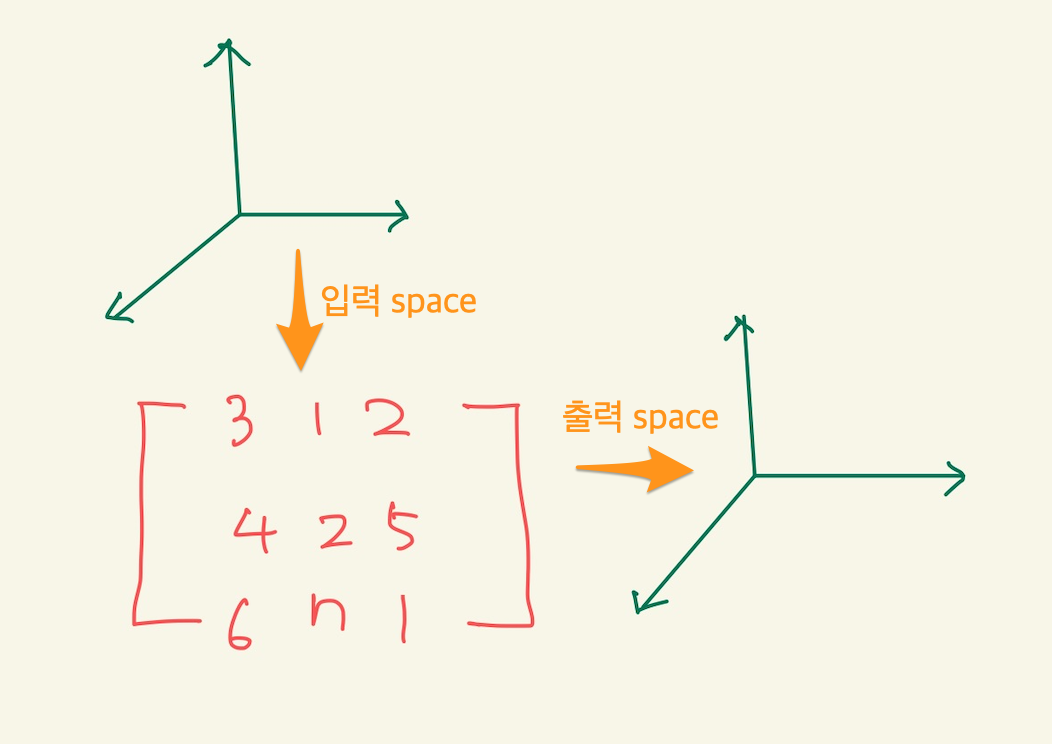
Figure 6: feature space
우리가 가진 data를 가지고 machine을 만들었을때, machine을 행렬로 표현했었다.
\(H(\theta)=\) \(\theta_{0}\) \(+ \theta_{1}x_{1}\) \(+ \theta_{2}x_{2}\) \(+ \theta_{3}x_{3}\) \(+ \theta_{4}x_{4}\)
\(H(\theta)=\) \(\begin{bmatrix} \theta_{0} \\ \theta_{1} \\ \theta_{2} \\ \theta_{3} \\ \theta_{4} \end{bmatrix}^{T}\) \(\begin{bmatrix} x_{0} \\ x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{bmatrix}\)
여기서 feature space는 data의 space로 보고, machine의 입력공간이라고 본다. 즉, 다음과 같이 볼 수 있다.
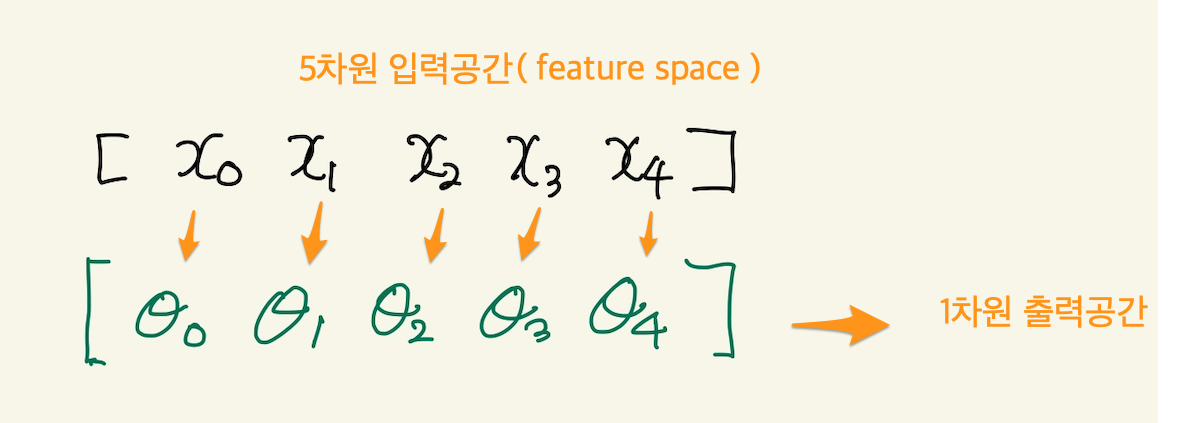
Figure 7: feature space3
data분포의 중요성
입력공간인 feature space가 주어지면 linear regression에선 예측이 잘 될것인지 아닌지를 feature space만 보고도 알수 있다. classification도 마찬가지인데, feature space를 보고 decision boundary를 그을수 있다면 잘 분류 할 수 있는지 없는지를 알 수 있다. 다음 그림을 보자. classification문제에서는 data의 분포를 보고 decision boundary를 쉽게 알 수 있고, 어떻게 하면 분류를 할수 있다고 예측을 할수 있다. linear regression에서 data분포를 보고 hypotheis function 결정한다. 즉 data분포가 매우중요하다. 아래그림은 classification인데 여기서도 분포가 대단히 중요하다.
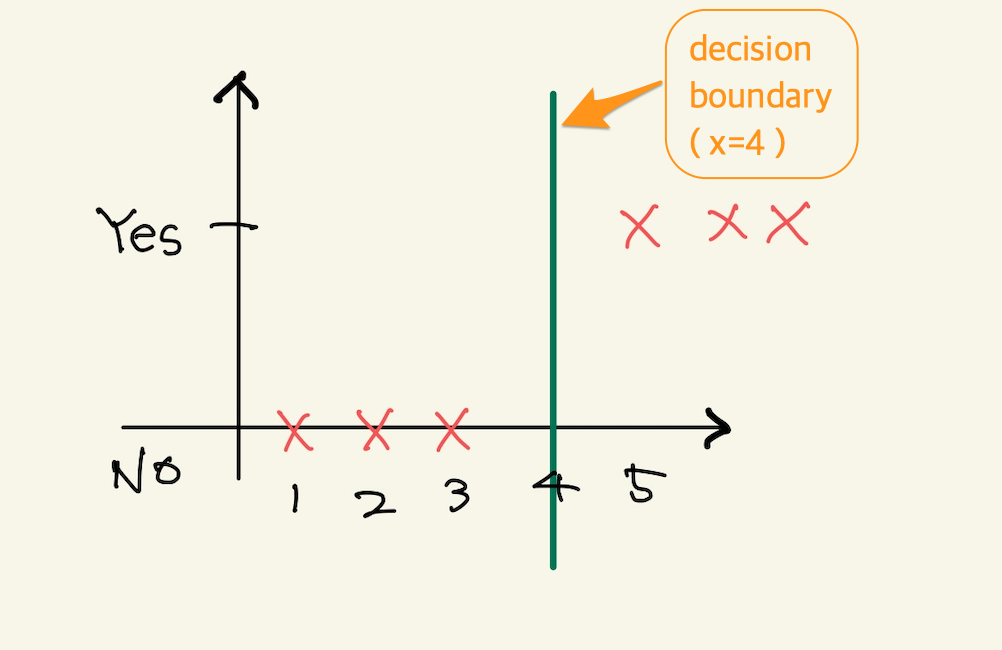
Figure 8: decision boundary1
위에서 x=4라는 decision boundary로 분류가 가능하다. 이런 데이터만 존재한다면 분포도만 보고서 machine learning을 사용하지 않아도 된다고 판단할 수 있다. 그정도로 data분포가 중요하다. 물론 machine learning을 사용하지 말라는 말은 아니다. 사용하면 매우 높은 정확도를 가진 machine이 될 것이다.
다음 그림도 보자.
feature scaling 개요
feature scaling은 feature space와 연관이 있다. feature space를 이루는 각축의 단위차가 크다면 feature space의 모양은 달라지고 이것은 학습에 영향을 미친다. feature scaling에 관한 좋은 설명이 있어서 덧붙인다. 참조:https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-8-Feature-Scaling-Feature-Selection

Figure 9: feature scaling
각각의 feature가 가진 범위가 있고, 다른 feature의 범위가 압도적으로 크다면, 예측에 영향을 미친다. 강사는 이것을 우리의 data와 연결지어 설명한다. 즉, 방의 개수와 방의 사이즈라는 두개의 feature를 볼때, 방의 size의 단위가 크기 때문에, 기울기를 update할때 영향을 미친다는것을 그래프로 설명한다. 이건 사족이긴 한데, feature(기울기)가 사용되는 곳은 2가지가 있다. 첫번째로 예측값계산, 두번째 경사하강법이다. 경사하강법을 들으면 이 식이 생각나야한다. 새로운기울기 = 옛날기울기 - (learning_rate)(미분값). 강사의 그래프를 보자.
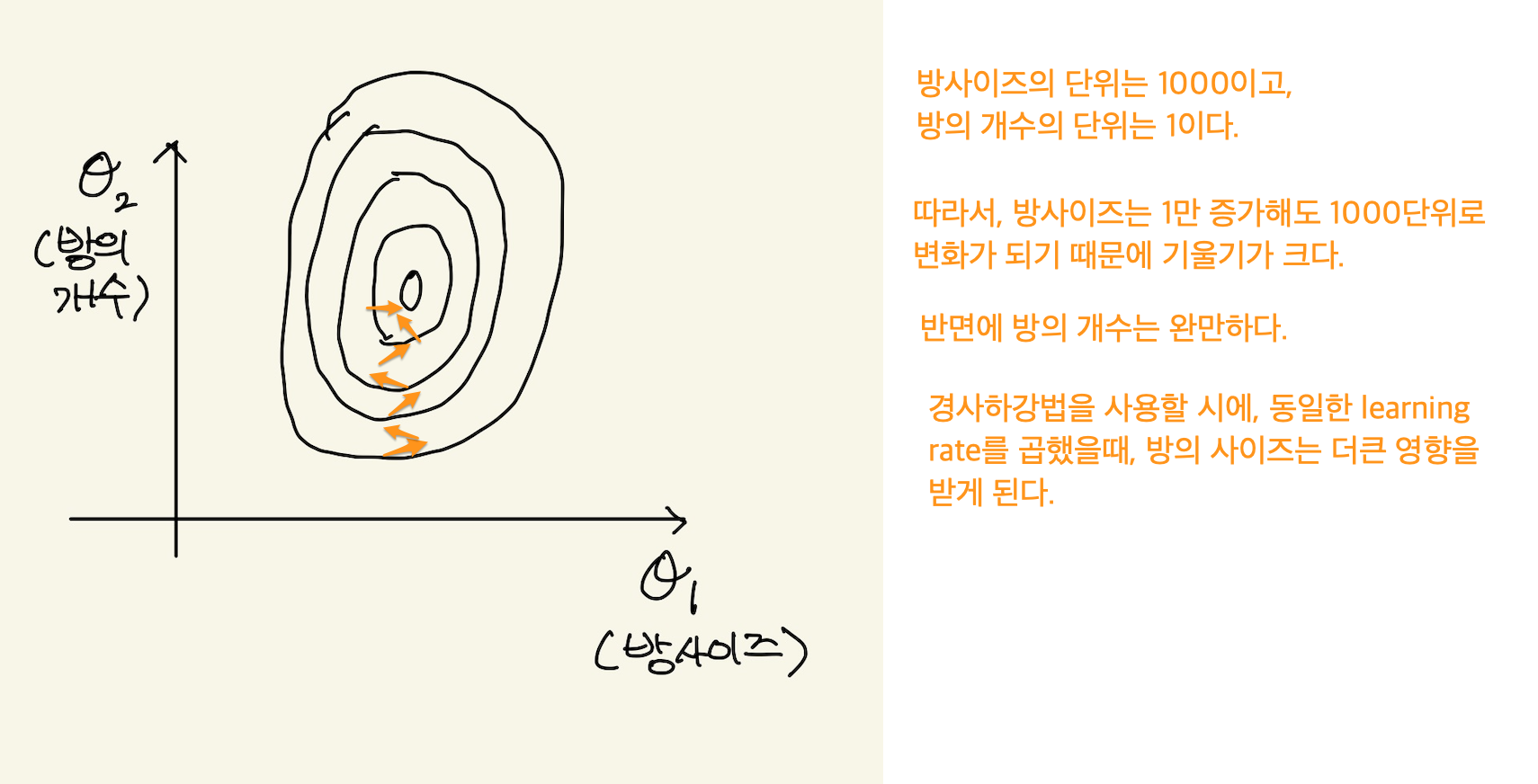
Figure 10: feature scaling2
feature의 범위가 크면, 기울기도 급격해서 기울기를 update할때, 동일한 learning rate를 곱하면 더많은 변화가 있다고 한다. 위의 그래프를 보는 법을 강사가 설명하는데 도움이 될까 해서 적어본다.
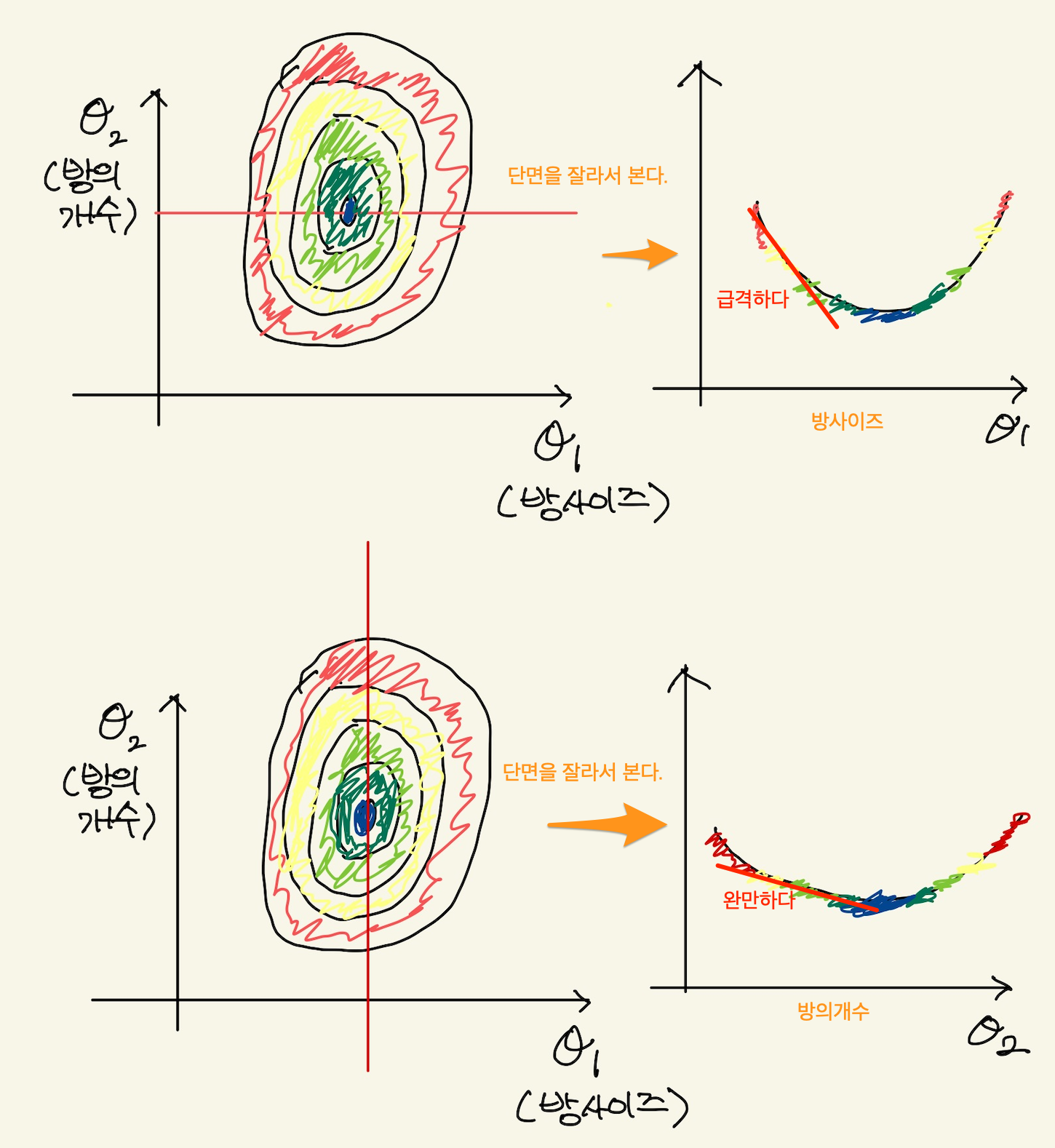
Figure 11: feature scaling3
강사의 설명은 단면을 잘라서 기울기를 확인할 수 있다고 한다. 기울기가 완만한것은 거의 0에 가깝기 때문에 learning rate를 곱해도 의미가 없다. 반면 기울기가 급격한것은 learning rate를 곱하면 급격히 증가한다. 즉 feature의 범위가 작으면 기울기의 이동이 매우 작다. 이것은 기울기 변화에 매우 둔감해진다. 또, feature의 범위가 크면 기울기의 이동이 매우 커지게 된다. 이 경우는, 기울기 변화에 매우 민감하게 된다. 기울기 민감도는 아래 그림을 보자.
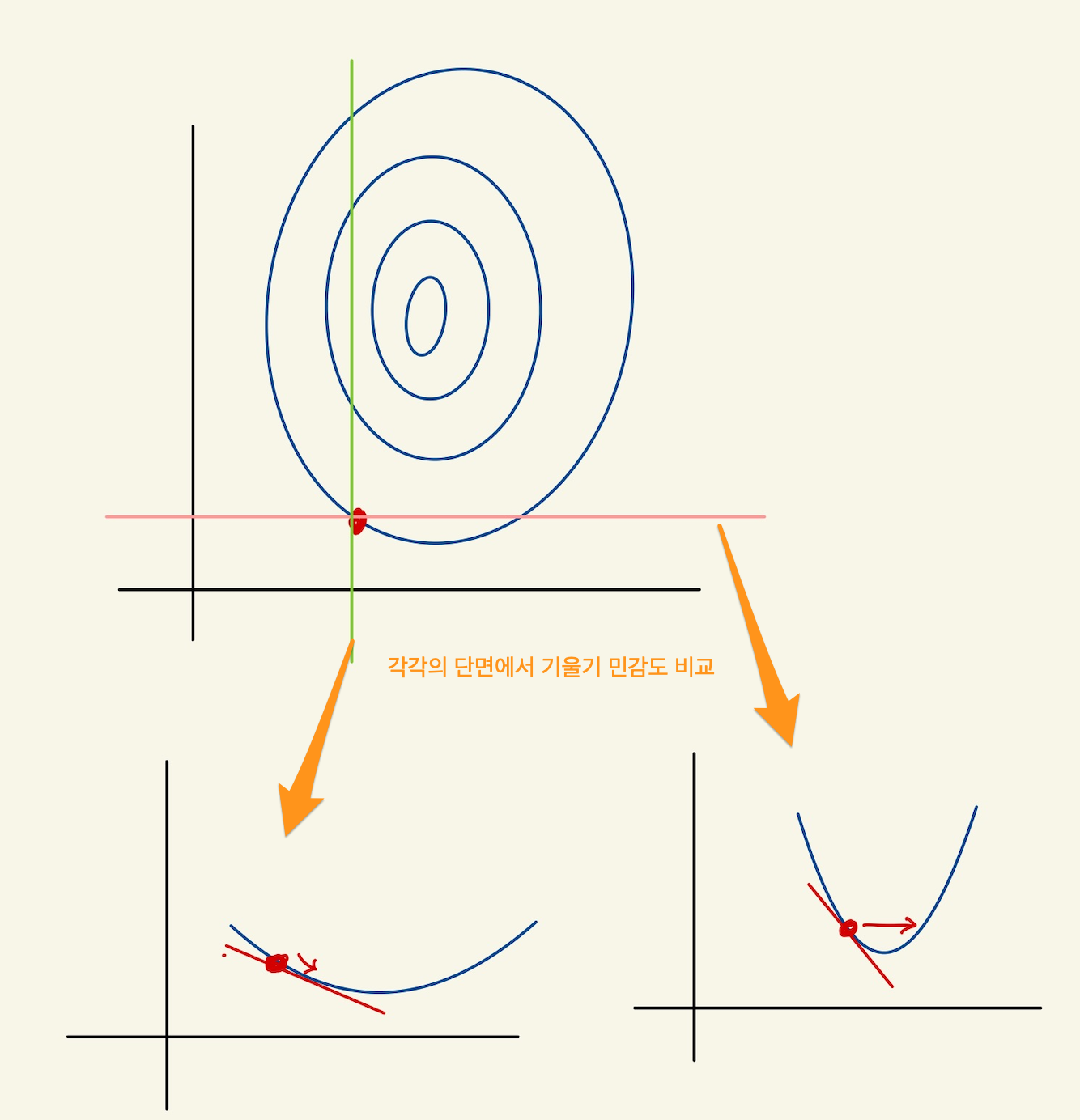
Figure 12: feature scaling
기울기가 급격하면, 동일한 step size(learning rate)에 대해서 많이 이동하고 기울기가 완만하면 적게간다는 것이다. 이것을 수정하려고 한다.
feature scaling
feature space에서 각각의 feature 범위 때문에 학습에 문제가 있다는 것을 알았다. 이 문제를 해결하려고 한다. 아래 그림처럼 만들어 문제를 해결하려고 한다.
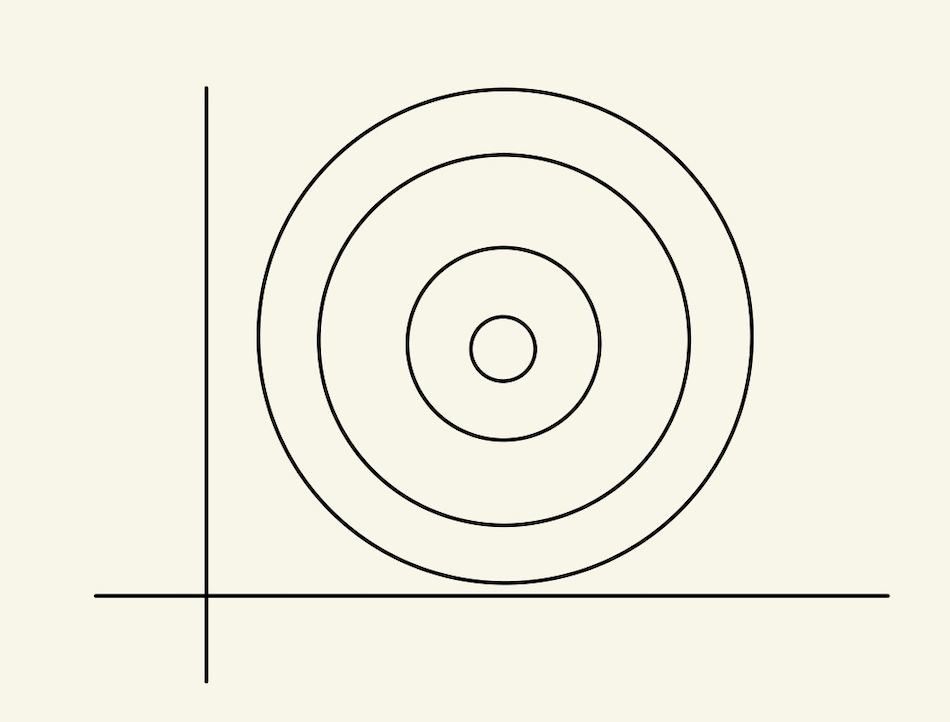
Figure 13: feature scaling5
가장 쉬운 방법은 data에서 가장 큰 값으로 나누는 방식이다. 즉, 값을 예를들어서, 다음과 같은 데이터를 보면, machine을 만들기전에 data를 좀 살펴봐야 한다. 아 이거, size가 너무 큰데라고 보고 feature scaling이 필요하다고 생각할 수 있어야 한다.
| size | number of bedrooms | number of floors | Age of home | Price |
|---|---|---|---|---|
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
size의 data중 가장 큰 data인 2104로 모든 값을 나눠준다. bedrooms도 마찬가지다. 가장 큰값인 5로 나눠준다.
-
size
\(\theta_{0}^{[1]}\) = \(\cfrac{2104}{2104}\)
\(\theta_{0}^{[2]}\) = \(\cfrac{1416}{2104}\)
\(\ldots\)
- bedrooms
\(\theta_{1}^{[1]}\) = \(\cfrac{5}{5}\)
\(\theta_{1}^{[2]}\) = \(\cfrac{5}{5}\)
\(\ldots\)
가장 큰값으로 나눠주기 때문에 최대값은 모든값은 1이하가 된다.
feature scaling [0~1 사이의 값]
위의 예가 최대값을 고려한다고 한다면, 최대값과 최소값을 고려할 수도 있다. 이전 방법은 최대값이 1이라서 나머지 모든 데이터가 1이하의 값이 되었다. 그러면 -900도 있을 수 있다. 그래서 0~1 범위를 갖게 할려고한다. 아래와 같은 데이터가 있다고 하자.
| size | number of bedrooms | number of floors | Age of home | Price |
|---|---|---|---|---|
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
그러면, size를 0-1값을 갖게 하려면, 어떻게 해야할까? 방법이 있다.
- 가장 작은값을 찾는다. => 852 이다.
- 가장 작은값을 모든 data에서 빼준다. => 2104-852 = 1252 => 1416-852 = 564 … => 852 -852 =0
- 이제 가장 큰값으로 나눠준다. => 1252/1252 =1 => 564/1252 = 0.43 … => 0/1252 =0
- 이렇게 해서 모든 data를 0과 1사이 값으로 만들 수 있다. 이게 normalize다. 학습전에 이런 normalizing을 한다.
feature scaling [-1~1 사이의 값]
위와 같은 데이터가 있다고 하자. 똑같이 size값을 -1과 1사이의 값으로 나타내보자.
| size | number of bedrooms | number of floors | Age of home | Price |
|---|---|---|---|---|
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 1534 | 3 | 2 | 30 | 315 |
| 852 | 2 | 1 | 36 | 178 |
이것은 평균값을 이용해서 계산한다.
- 평균값을 구한다. => (2104+852)/2 = 2956/2 = 1478
- 모든 data에 1478을 빼준다. => 2104-1478 = 626 … => 852-1478 = -626
- data의 최대값과 최소값은 동일한 값이지만 부호만 다르다. 이때, 평균값으로 나눠주면 된다. => 626/626 = 1 … -626/626 = -1
- 이렇게 해서 -1과 1사이의 값으로 나타낸다.
feature scaling 범위를 만드는 일반식
0~1의 범위
data를 특정범위의 값만을 사용하는 feature scaling을 하는 일반적인 방법이 있다. 다음과 같은 data가 있다고 하자.
3 -1 7
최대값 7을 1로 만들고, -1이란 최소값을 0으로 만들고 싶다고 하자. 이것은 1차방정식으로 푼다.
y = ax +b case x=1: -a + b = 0 case x=7: 7a + b = 1
\(a = \cfrac{1}{8}\) , \(b = \cfrac{1}{8}\)
\(y =\cfrac{1}{8}x +\cfrac{1}{8}\)
두개를 연립해서 1차 방정식을 만들었다. 이 방정식으로 어떤 값이던지 0과 1사이로 만들 수가 있다.
-1~1 범위
이것도 방정식으로 해결한다. 아래와 같은 data가 있다고 하자.
2,3,5,3,2,2
최대값인 5는 1에 mapping되고, 최소값 2는 -1에 mapping되게 하면 된다.
y = ax + b
case x=2: 2a +b =-1 case x=5: 5a +b = 1
\(a = \cfrac{2}{3}\) , \(b= \cfrac{7}{3}\)
\(y = \cfrac{2}{3}x + \cfrac{7}{3}\)
위 방정식으로 모든 data의 값을 -1과 1 사이로 만들수가 있다.
feature scaling - standardization(mean normalization)
normalization은 data를 0과 1사이의 값으로 feature scaling한다. standardization란 용어는 normalization과 비슷하지만 통계에서 유래한다. 표준화, 표준편차 같은 통계적 용어다. 그래서 평균과 분산을 사용해서 data들을 scaling한다. 어떤 data가 주어지면 평균과 분산을 구할 수 있다. 예를 들어보자.
1800, 2200, 1650, 2350
이것의 평균은 2000이다. 그리고 분산은 공식에 의해서 구해진다.
\(\cfrac{(1800- average)^{2} + (2200- average)^{2} + (1650- average)^{2} + (2350- average)^{2}}{4}\)
standardization은 data의 평균과 분산을 아래 그림처럼 만드는 것이다. 평균은 0, 분산은 1로 만든다.
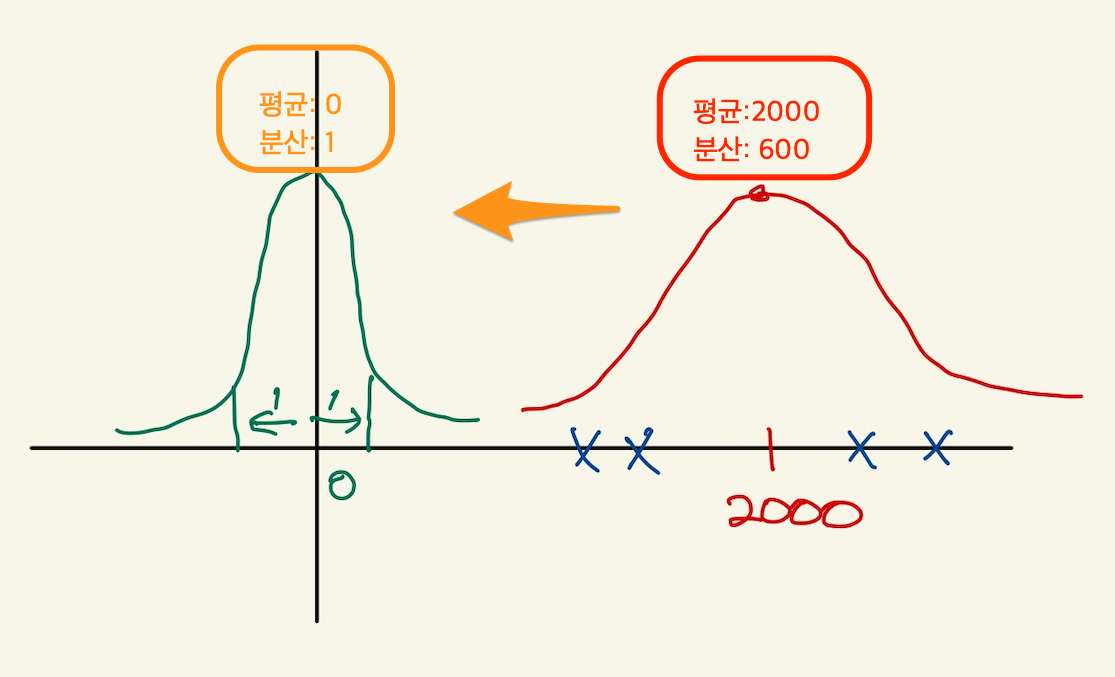
Figure 14: feature scale6
outliar 문제
평균과 분산으로 feature scaling을 하는것은 이전의 range로 feature scaling하는 것보다 더 장점이 있다. 이전 방식이 outliar에 취약점이 있기 때문이다. outliar란 튀는놈을 말한다. 예를 들어서, 집평수 data가 대부분 10-50사이 값인데, 갑자기 3000평이라는 데이터가 오게 되면, range 0-1로 feature scaling하게 되면, 대부분의 집평수값은 0값을 갖게 되는 문제가 생긴다. 그림으로 본다면 다음과 같다.
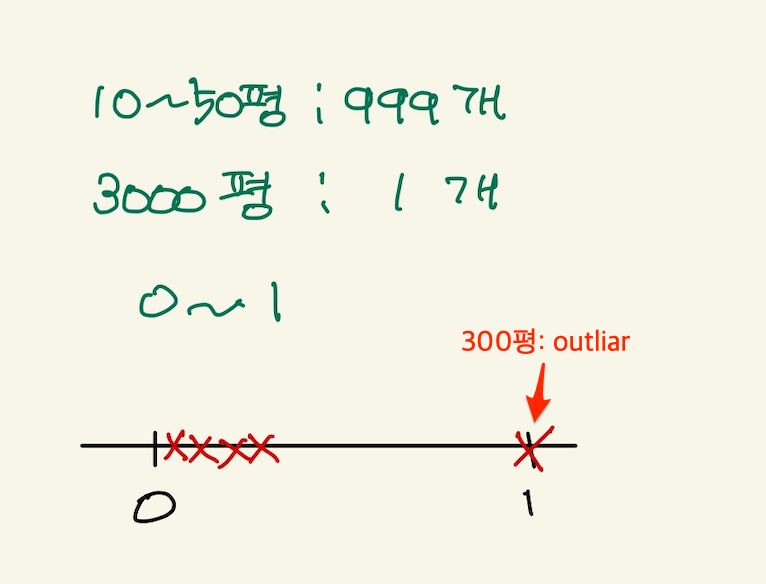
Figure 15: feature scaling7
range로 feature scaling하는 것은 outliar에 취약하다.
