[machine learning] day18-logistic-regression
Logistic Regression
logistic regression이란 무엇이냐?
이 강의에선 분류 문제를 다룬다. 분류는 yes or no로 분류하는 것을 말한다. 분류가 2개면, binary classification이라고 부르고, 여러개로 분류하는 것을 multi-class classification이라고 한다. binary class에서 no,negative는 0으로 yes,positive는 1로 표시한다.
feature space와 model
logistic classification은 0과 1의 정답을 가진다. 이런 정답을 모델의 예측치로 나타내려면, 모델이 data분포도와 얼추 맞아야 학습을 통해서 fitting이 가능한데, 그렇게 하기위해선 예측값이 0 or 1이 나와야 모델을 근사화할 수 있다. 그렇게 하기위해선 step function이 가능한데, 그것은 미분 불가능하다. 그래서 sigmoid를 사용한다. linear regression에서도 model을 feature space에 fitting하기 위해서 model에 제곱이나 제곱근을 넣었던것과 연관되는 설명이다.
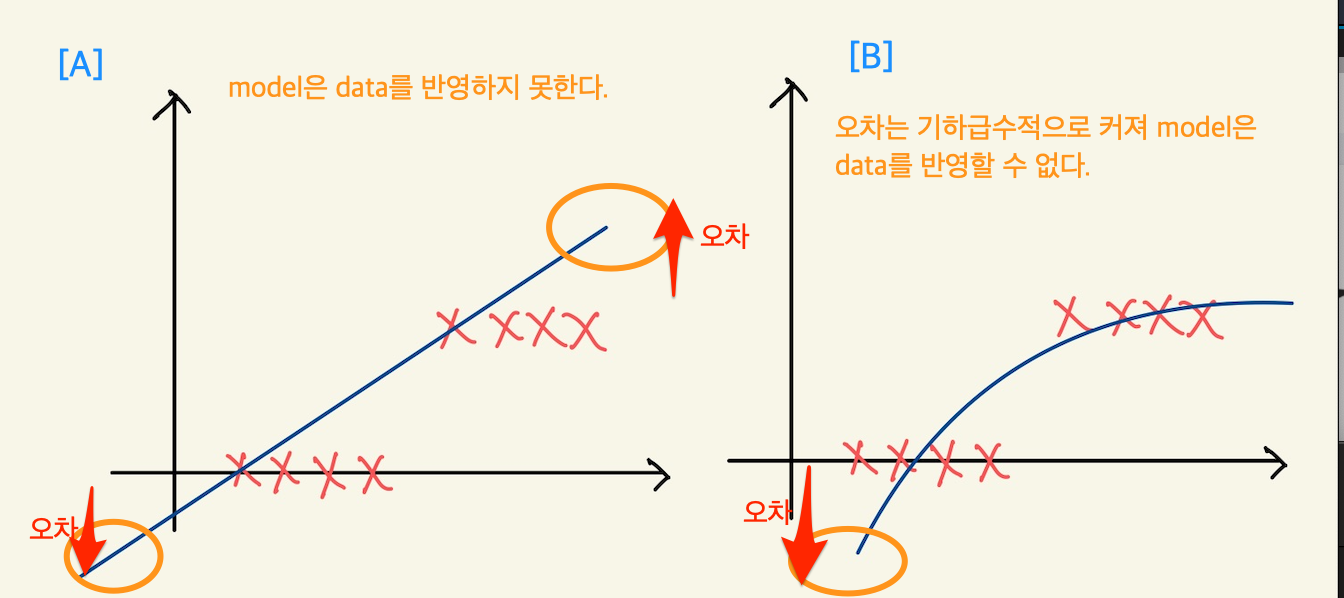
Figure 1: logistic regression feature space
A에서 보면, 1차식의 linear regression에서 사용한 model을 사용하면, 예측치와 정답의 차이가 양 극단으로 갈 수록 커진다는 것을 알 수 있다. B에서는 model에 제곱근을 넣어서 완만한 기울기를 갖게해서 예측치가 1이 나오게 시도했지만, 이 경우도 오차가 커져서 model이 data의 정답분포에 fitting하지 않는다.
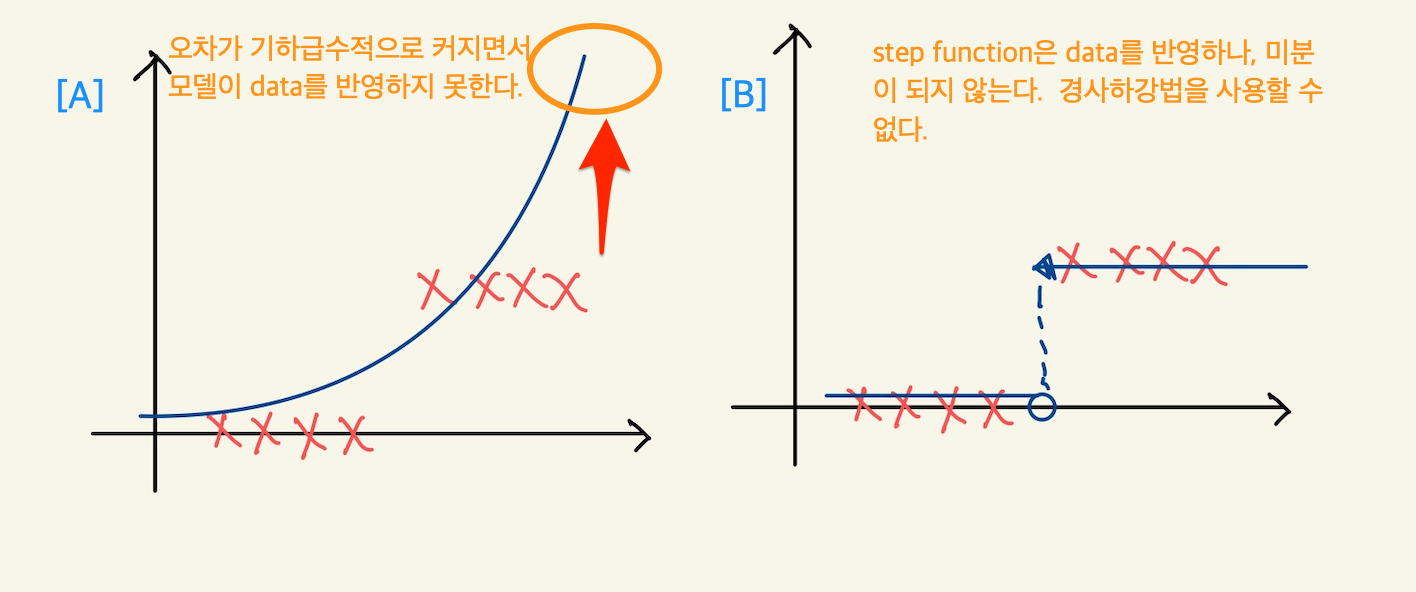
Figure 2: logistic regression feature space2
여기서의 A는 linear regression에서 본 제곱값이 model에 포함된 경우다. 이 경우도 마찬가지로 오차가 갈수록 커지게 된다. B는 step function이라서 가장 적절한 model이긴 하나, 미분이 안된다는 문제가 있다.
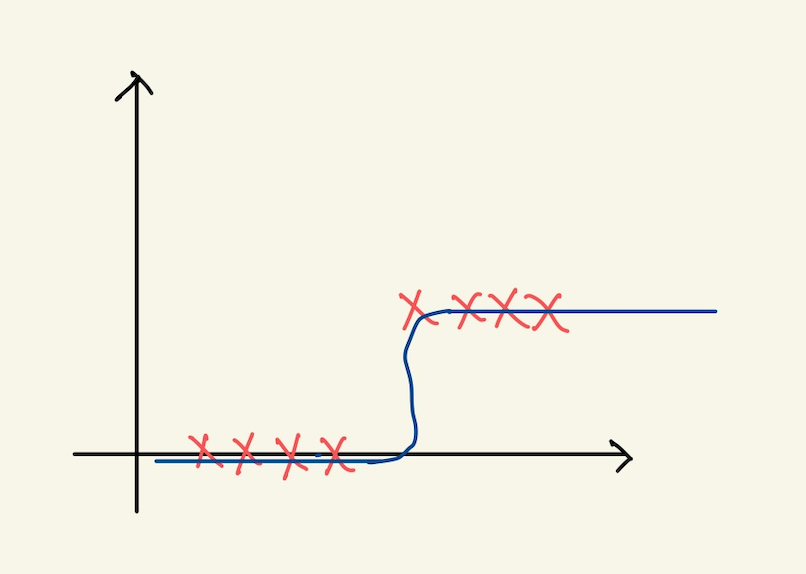
Figure 3: logistic regression feature space3
이것이 sigmoid function이라고 해서 미분도 가능하고, 예측치가 데이터의 모양과 가장 잘 fit할 수 있다.
linear regression model과 logistic problem
강사는 우리가 이전 배웠던 linear regression model, 1차직선으로 답이 0과 1에 해당하는 문제를 해결할 수 없음을 얘기한다. 내용의 핵심은 직선을 아무리 경사하강법으로 오차가 가장 작은, 직선의 기울기를 만들었다고 할 지라도, machine의 성능은 좋을 수가 없다는 것이다.
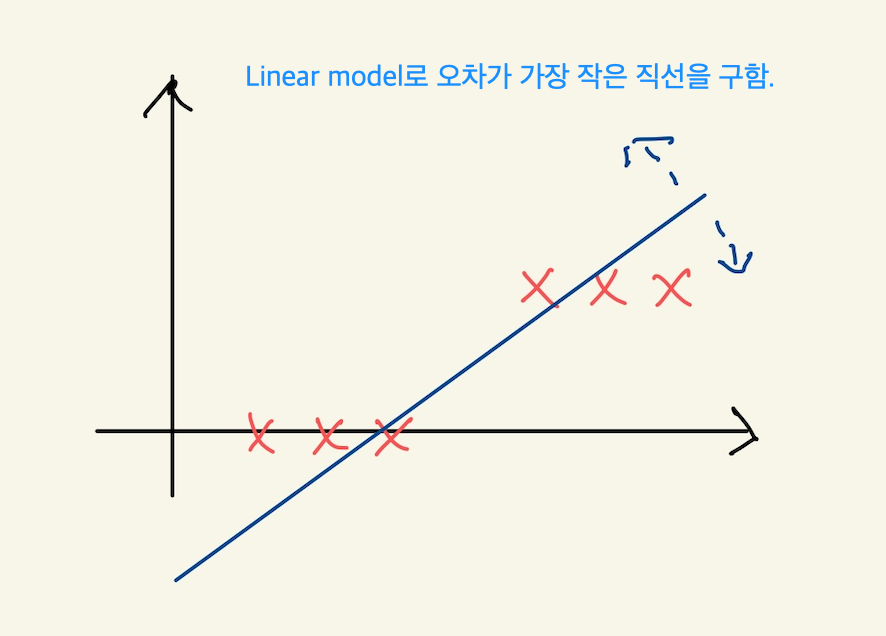
Figure 4: logistic4
machine이 아무리 직선을 이리 저리 돌려서 최적의 직선을 찾아냈다고 해도, 선형 모델은 에러가 여전히 크다. 즉 좋은 machine을 애시당초 만들수가 없다는 것이다.
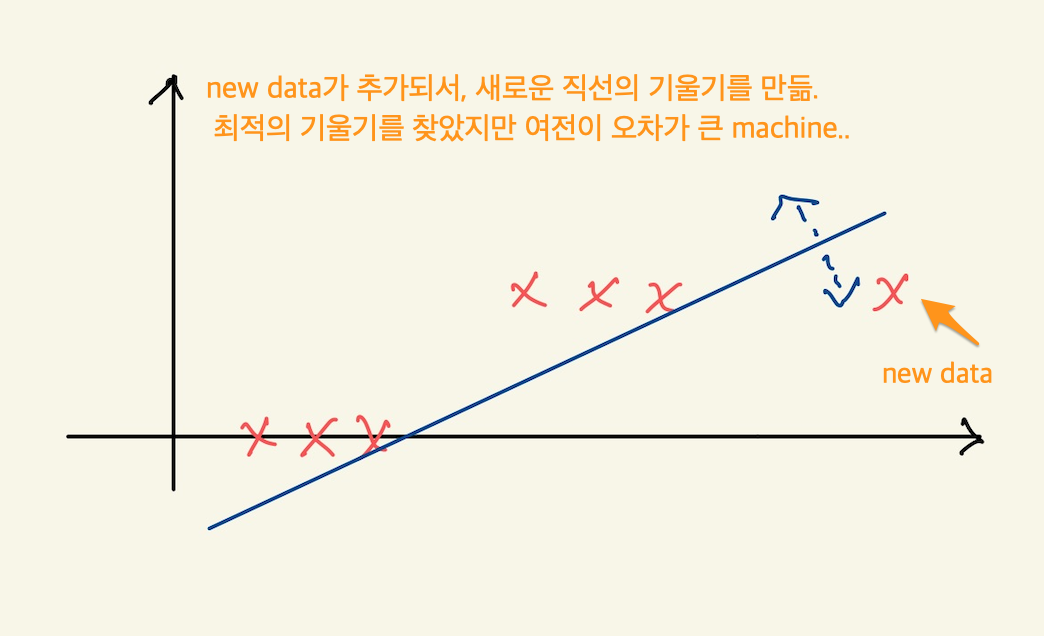
Figure 5: logistic5
새로운 데이터가 추가되서, 추가된 데이터를 가장 잘 예측할수 있는 machine을 만들어도 선형 모델의 한계로 예측의 정확성은 매우 떨어진다. 새로들어온 data를 예측한다고 할때, 현재 모델의 예측값은 매우크다. 100이라고 한다면, 정답은 1이기 때문에 99의 오차가 있는것이다. 즉 model을 선형모델을 쓰면 안된다. 가장 좋은것은 step function과 같아야 한다. 그래야 새로운 데이터가 주어졌을 때, 1이란 값을 예측할 수 있다. 그것과 가장 비슷한게 sigmoid function이다.
sigmoid function
sigmoid function의 식은 다음과 같다.
\(S(x)\) \(=\cfrac{1} {1+e^{-x}}\) \(=\cfrac{e^{x}}{e^{x}+1}\)
그래프는 다음과 같다.
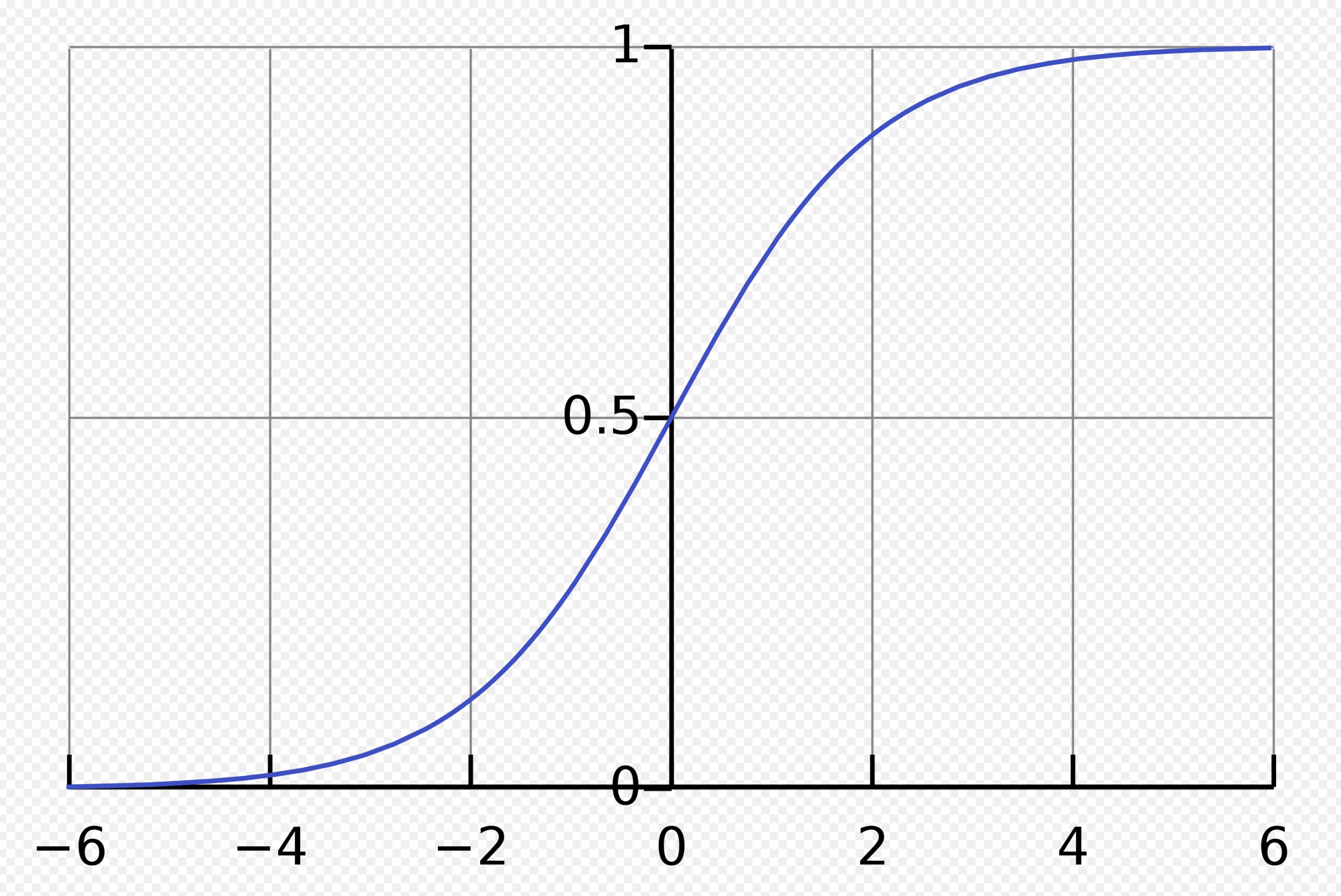
Figure 6: sigmoid
여기에서 x에는 matrix형태의 model이 연결된다.
logistic model
sigmoid 함수가 classification data, 특히 binary데이터에는 매우 적합하다는 것을 알 수 있었다. 그러면 sigmoid를 바로 우리의 모델로 하면 되지 않을까? 안된다. 왜냐면 우리가 입력으로 받는 feature space의 feature들은 1개가 아니라 수십개 수백개 되기 때문에, 차원이 많은 입력공간을 처리하기 위해서는 matrix형태의 model이 되어야 하기 때문이다. 그리고 그런 입려공간의 feature들을 수정해야 하기 때문에 sigmoid를 바로 model로 사용할 수 없다. matrix형태의 model을 그대로 사용하고, sigmoid function을 마치 adapter마냥 끼워넣는 합성함수 형태로 사용한다. 즉 matrix형태의 model이 출력하는 값을 sigmoid함수가 입력으로 받아서 0-1 사이의 값을 출력하는 형태다.
일반적인 linear model은 다음과 같았다.
\(Z=\) \(Q^{T}X\)
여기에 sigmoid function을 결합하면 최종 model은 다음과 같다.
\(H =\) \(\cfrac{1}{1+e^{-Z}}\) \(= \cfrac{1}{1+e^{-(Q^{T}X})}\)
decision boundary
feature가 1개인 one-variable classification에서 decision boundary
logical model을 만들었다. logical model은 두개의 함수를 합성함수로 연결한것이다. 직선에 관한 function과 sigmoid function을 합성함수로 만들어서 나온 결과는 0이나 1의 값이 아니다. data에서는 정답이 0이나 1의 값인데, model의 값은 0에서 1사이의 값이다. 만일 0.7이 나온다면, 이값을 1로하겠다. 그리고 만일 예측치가 0.3이 나온다면, 0으로 하겠다라고 결정할 수 있어야 한다. 결정을 하기 위해선 기준이 되는 값이 필요하다. 그것이 decision boundary다. 예를 들어서 0.5이상은 1로 하겠다. 0.5이하는 0으로 하겠다는 결정을 할 수 있어야만 예측값을 말할 수 있다. 즉,
\(H(Z) > 0.5 => 1\)
\(H(Z) < 0.5 => 0\)
0.5를 기준으로 하는 이유는 sigmoid함수의 중간값을 기준으로 삼기 때문이다.

Figure 7: sigmoid
그러면 우리가 machine의 모델을 만들 때, 선형결합으로된 1차함수를 만들고, 그것의 값을 0과1사이로 표현할 sigmoid함수를 만들고, 다시 decision boundary에 따라서 결정할수 있는 decision function을 만들어야 하는가? 3개의 function을 합쳐서 model을 만드는가?
그런데, decision boundary는 H(Z)의 값만을 기준으로 정하지 않아도 된다. Z값을 기준으로 정할 수 있다. Z가 0일때 H(Z)가 0.5가 되고 H(Z)가 0.5다 클때를 1, 작을때를 0으로 해서 decision boundary를 설정하는것은 Z 기준으로 보면, Z가 0보다 클때 1, 작을때를 0으로 판단하는데,즉, 0을 decision boundary로 본다. H(Z)에서 decision boundary가 0.5라고 했으면 됐지, 왜 Z기준으로 다시 decision boundary를 말하는가? 이것은 data에 따른 예측값을 바로 알 수 있다. H(Z)를 다 계산하고 0.5보다 큰지 작은지를 따져서 아는게 아니라, machine에 초기값이 주어지면, Z함수를 만들수 있는데, 이함수에 data를 넣으면 예측치를 바로 계산이 가능하게 된다. 왜냐? Z값이 0보다 크면 1, 0보다 작으면 0으로 바로 판단할 수 있기 때문이다. 물론 H로 예측할수도 있다. 그러나 Z나 H가 예측값이 같다. 그러면 H에 있는 sigmoid함수의 역할 왜 필요한가?에 대한 질문을 할 수 있다.우리가 원하는건 예측하는 기계고 Z만 계산해서 boundary가 0보다 크냐 1보다 크냐로 예측값을 출력하면 되는 것 아닌가? cost function과 연관이 있다는것은 알 수 있다. 새로운 기울기를 설정할때, 오차계산이 필요한데, Z만 사용하면 오차가 엄청 커지기 때문이다. 그래서 sigmoid가 필요하다는 건 알겠다. 이것과 관련되서는 경사하강법을 공부할때 다시 정리해야 할듯하다. 그런데 한가지 Z함수는 feature space에서 decision boundary를 볼때, 직관적인 설명이 가능하게 해준다. 예를 들어보자.
feature가 1개인 data가 표로 주어지고 이것을 그래프로 표현한게 다음과 같다고 하자.
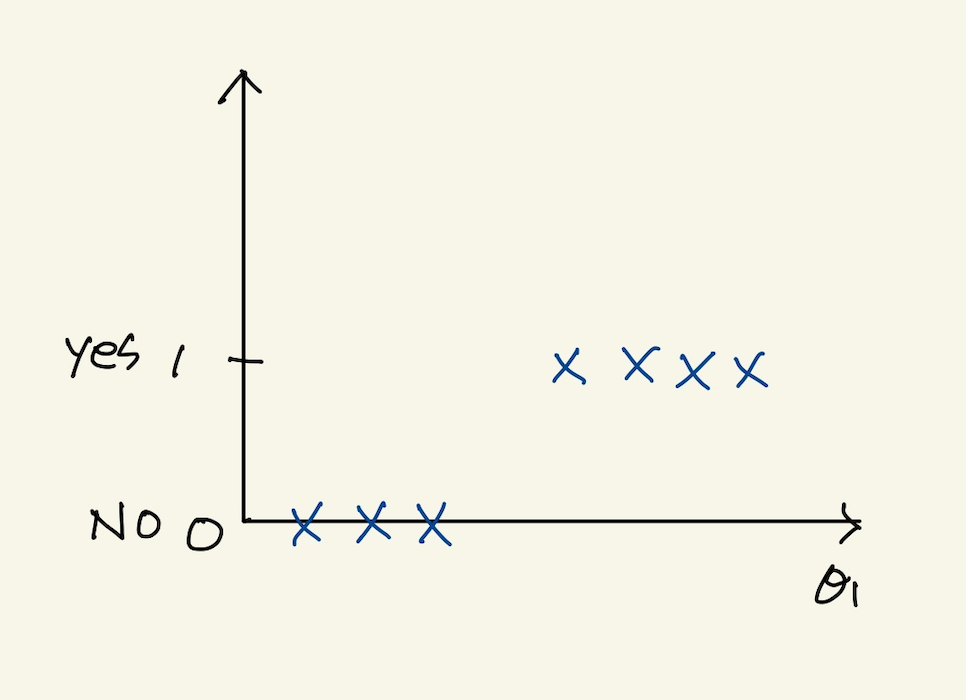
Figure 8: logical feature space
우리에게는 1차함수인 z는 다음과 같이 표시된다.
\(Z =\) \(\theta_{0}\) + \(\theta_{1}x_{1}\)
그것을 입력으로 받는 Hypotheis function도 다음과 같이 나타낼 수 있다.
\(H(Z)=\) \(\cfrac{1}{1+e^{-Z}\)
처음에 초기값으로 \(\theta_{0}\) 과 \(\theta_{1}\) 이 주어지고 경사하강법으로 기울기와 절편을 update해서 최적의 기울기와 절편을 구했다고 하자. 그때의 값이 Z= x -4라고 한다면, decision boundary는 Z가 0이되는 지점으로 나타낼 수 있을것이고, 그래프로 표시하면 x=4로 표시한다. 즉 x>4이면 1로 x<4으면 0인 decision boundary를 나타낸다. 즉 아래와 같은 그림이 될 것이다.
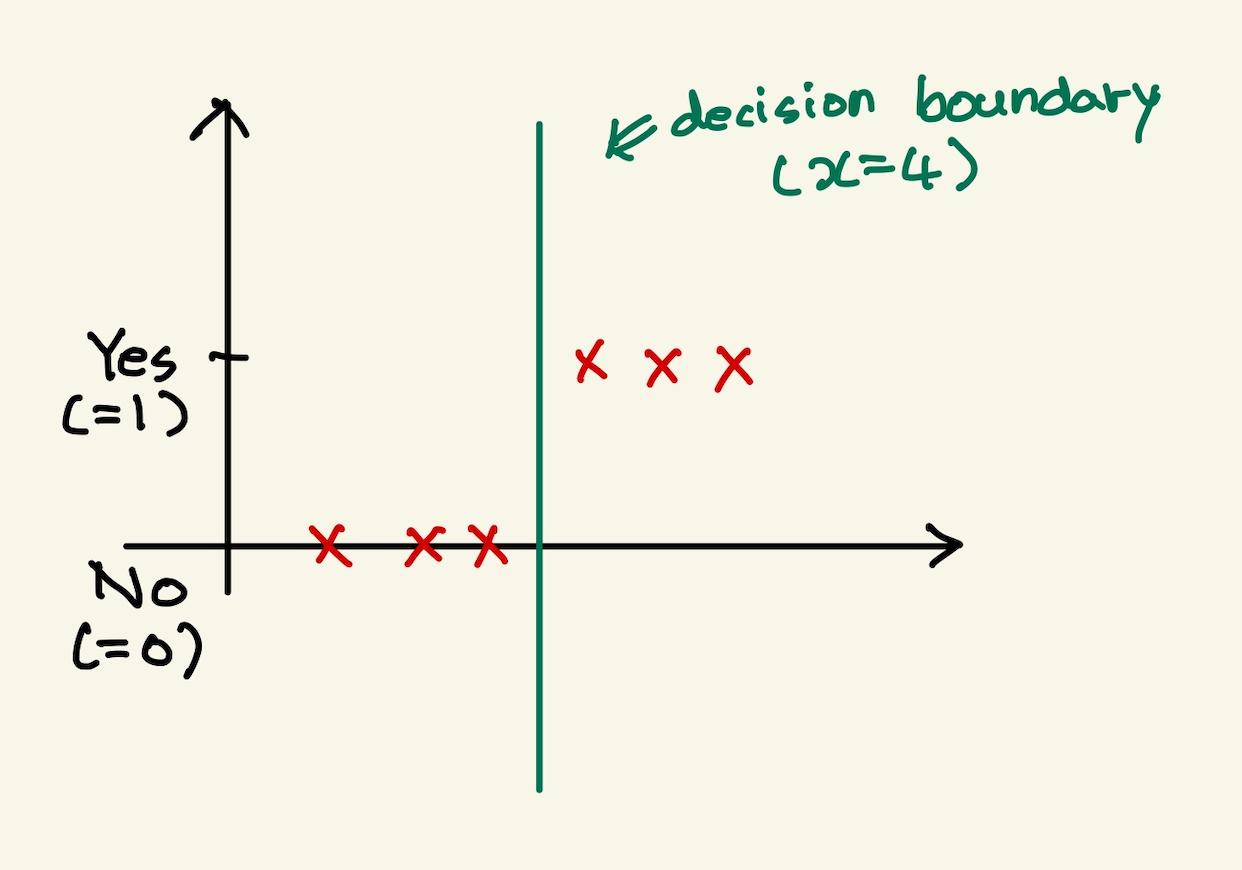
Figure 9: decision boundary
x=4에서 decision boundary가 된다.
cost function
machine에 대해
machine learning을 만드는데 있어서, machine만 보면, machine은 예측을 한다. parameter가 setting되고 데이터가 machine에 주어지면 예측을 한다. linear regression에서는 그렇다. classification에서의 예측은 좀 다르다. parameter가 주어지고 데이터가 주어지면, 예측치가 0-1사이의 실수값으로 나온다. 따라서 machine의 최종 예측값은 확률로 표시되는데, 이것을 decision boundary를 통과시켜서 0 또는 1의 값을 만들수 있다. 이것이 classification의 machine learning의 machine 기능에 해당한다.
learning에 대해
-
linear regression방식
cost function은 machine learning에서 learning에 포함된 기능이다. learning은 machine의 parameter를 update하는 것이다. 업데이트를 위해선 기준이 필요하다. 그 기준이 오차다. 결과와 예측치의 오차가 크면 많이 update하고, 적으면 적게 update한다가 기본 생각이다. 그 오차를 계산하는 함수를 cost function이라고 한다. cost function은 오차의 값만을 출력할 뿐이다. 즉 기울기 재설정이라는 learning의 핵심적 기능에 사용되는 기준을 제공할 뿐이다. cost function이 제공하는 오차를 보고, 오차가 크다, 작다를 판단하거나 그것을 값으로 나타내서, 이전 parameter를 새 parameter로 기울기 재설정 작업은 별도의 learning 기능이다. 예를 들면, gradient descent같은… linear regression을 예로 들어보자. linear regression에서 cost function은 parameter를 setting하고 machine을 돌리면 예측값이 나오고 정답과의 오차를 계산해서 cost function을 계산할 수 있었다. 그 계산값을 graph에 표시하고 다시 새로운 parameter를 설정하고 그 parameter에 따라서 machine을 돌리고 cost function값을 계속 표시하다 보니 cost function이 2차함수 형태의 그래프를 갖는다는 것을 알게 되었다. 그래프로 본다면, x축은 모델에서 나온값, 즉 예측치가 축으로 되고, 예측치마다 오차(cost)를 2차원 형태로 그리게 된다.
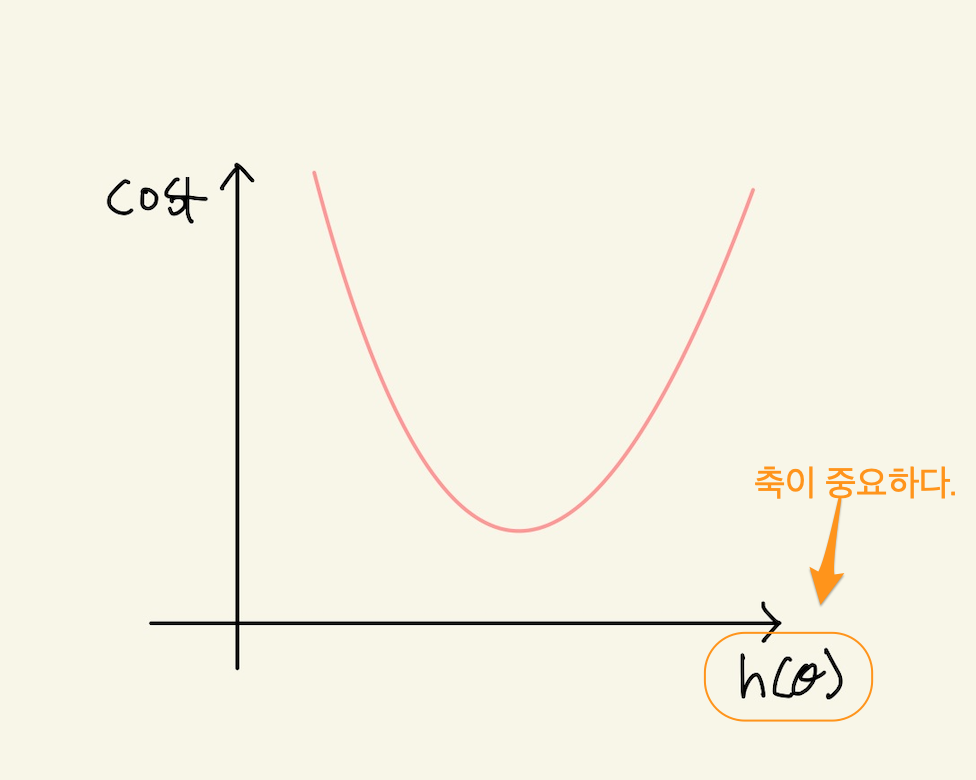
Figure 10: expected value
그래서 parameter를 넣고 machine을 돌려서 cost function값을 얻는게 아니라, cost function에, 예측치가 아닌 예측치를 계산하는 계산식을 넣어서 2차방정식을 얻을 수 있었다. 예를 들면 모든 데이터에 대해서 정답과 예측치(값이 아닌 parameter가 들어간)를 모두 더하면 2차식이 나온다. 그리고 그 2차방정식을 미분해서 미분식을 얻었다. 이게 매우 중요한 아이디어를 제공한다. 왜냐하면 learning의 핵심은 기울기 재설정인데, 기울기를 재설정하는것은 오차값이 아닌, 오차의 변화율을 이용하기 때문이다. cost function에서 계산된 오차값을 이용하면, machine은 계속 이전 오차값을 유지해야한다. 예를들면, 이전에는 오차값이 50였는데, 지금은 80나왔으니 30만큼 기울기를 재설정하는 하는 것이다. 그런데 미분식을 구할 수 있다면, cost function의 오차값을 매번 계산하지 않아도 된다. 오차값의 계산은 필요없다. 기울기를 재설정하는 learning의 핵심부분은 오차값이 아니라, 오차의 변화율이기 때문이다. 이게 gradient descent같은 방식에서 사용한다.
-
classification방식
parameter에 값을 넣지 않고, dataset의 데이터 개수만큼 다 돌려서 cost function을 얻고, 그 cost function의 미분식을 사용하자는 것이 linear regression방식이였다면, classification도 똑같이 할 수 있을까? 정답과 예측치의 차이가 cost function이라고 똑같이 정의한다면, 어떻게 될까? 즉 모든 데이터에 대해서 정답 - 예측치(\(H(\theta)\))를 계산해서 2차방정식으로 나타내면 되지 않을까? 하는 것이다. 그런데, linear regression과 달리 classification은 예측치가 좀 햇갈린다.
-
예측치
classification에선 예측값을 잘모르겠다. decision boundary를 통과한 값 0 or 1이 진짜 예측치 갖기도 하고, sigmoid function을 통과한 0에서 1사이의 값이 예측치 같기도하다. 어느게 예측값인지 알아야 정답과 예측치를 뺀 오차를 계산할 수 있을 것이다. 강사는 model을 통과한 값, 즉 sigmoid를 통과한 값이 예측치가 된다고 한다.
그러면 여기서 다시 cost function을 생각하자. linear regression에선 dataset에 대한 평균 오차값을 계산하는 함수가 cost function이였다. 그런데, classification에선 linear regression처럼 평균 오차를 계산하는 식으로 cost function을 정의하지 않는다. 왜냐면 dataset에 대해서 평균오차를 구하면 0-1사이의 값이 나오고, 다시 기울기를 변경하고 평균오차를 구해도 0-1사이의 값이 나온다. dataset에 10개의 data가 있다고 할때, 각 data의 최대 오차는 1이고 최소 오차는 0이다. 10개 모두 오차가 1이라고 하면 평균 오차의 최대값은 1이 된다. 그리고 평균오차의 최소값은 0이다. 매번 기울기를 변경하고 평균오차를 그래프로 찍는다고 하더라도, 2차함수처럼 곡선형이 나오는게 아니다. 미분가능한 곡선형이 아닌 끊어진 미분 불가능한 식으로 나오기 때문에, cost function의 미분식은 구할 수 없다. 그러면 경사하강법을 사용할 수 없기 때문에 cost function을 다른 방식으로 정의해야 한다. 즉 미분이 가능한 cost function으로 정의해야 한다.
-
classfication의 sigmoid에서 cost function까지 재정리
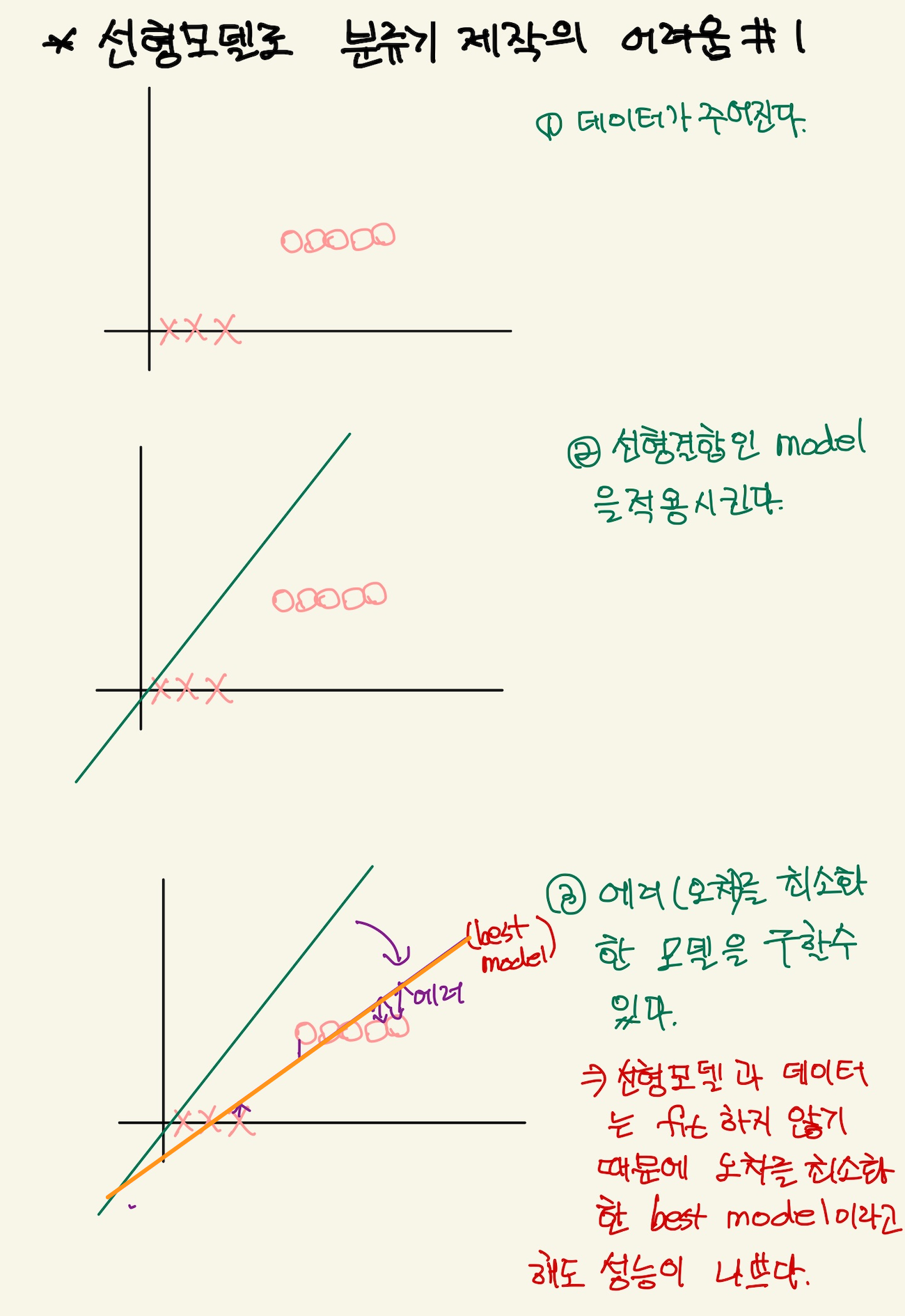
Figure 11: classification_1
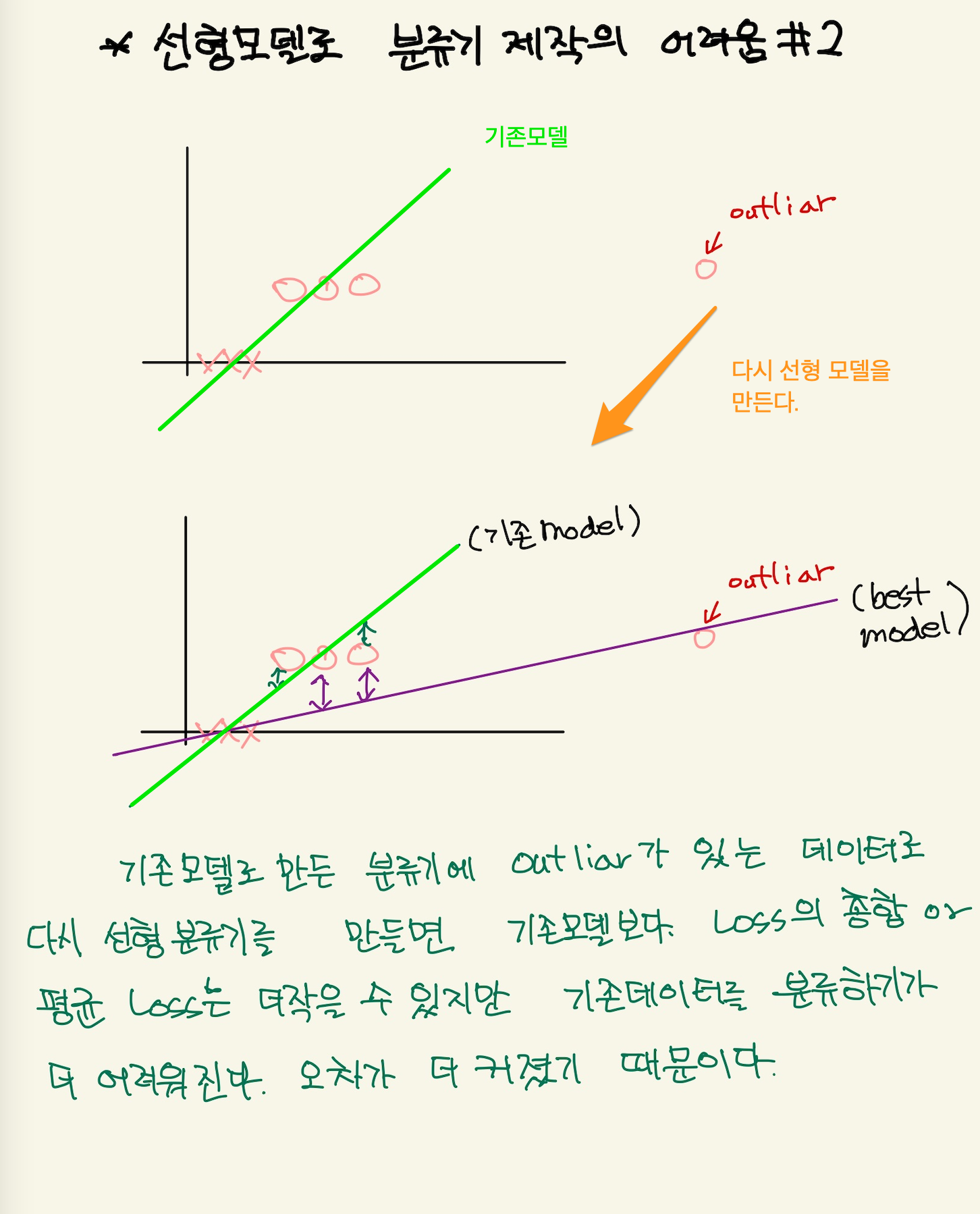
Figure 12: classification_2
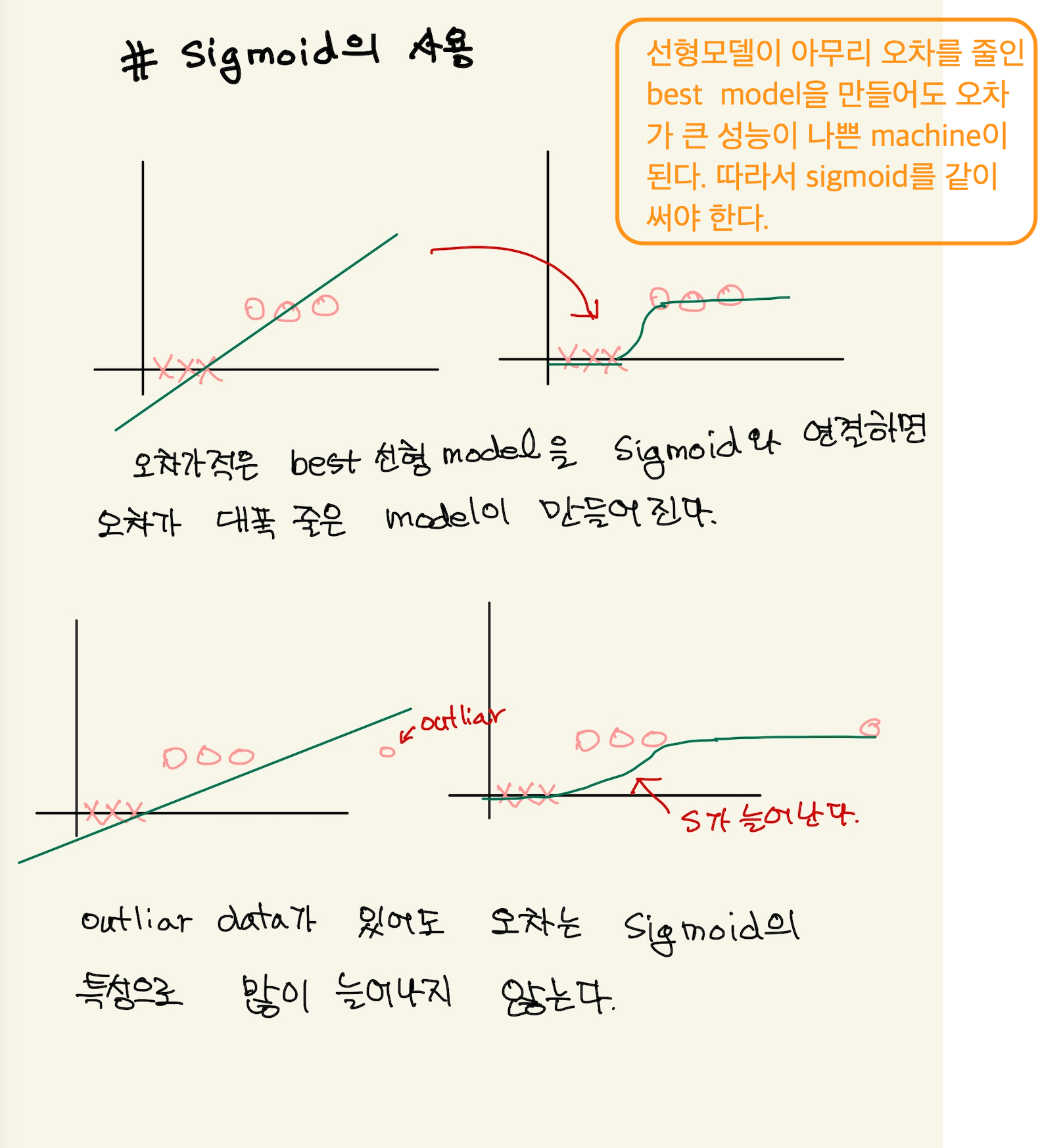
Figure 13: classification_3
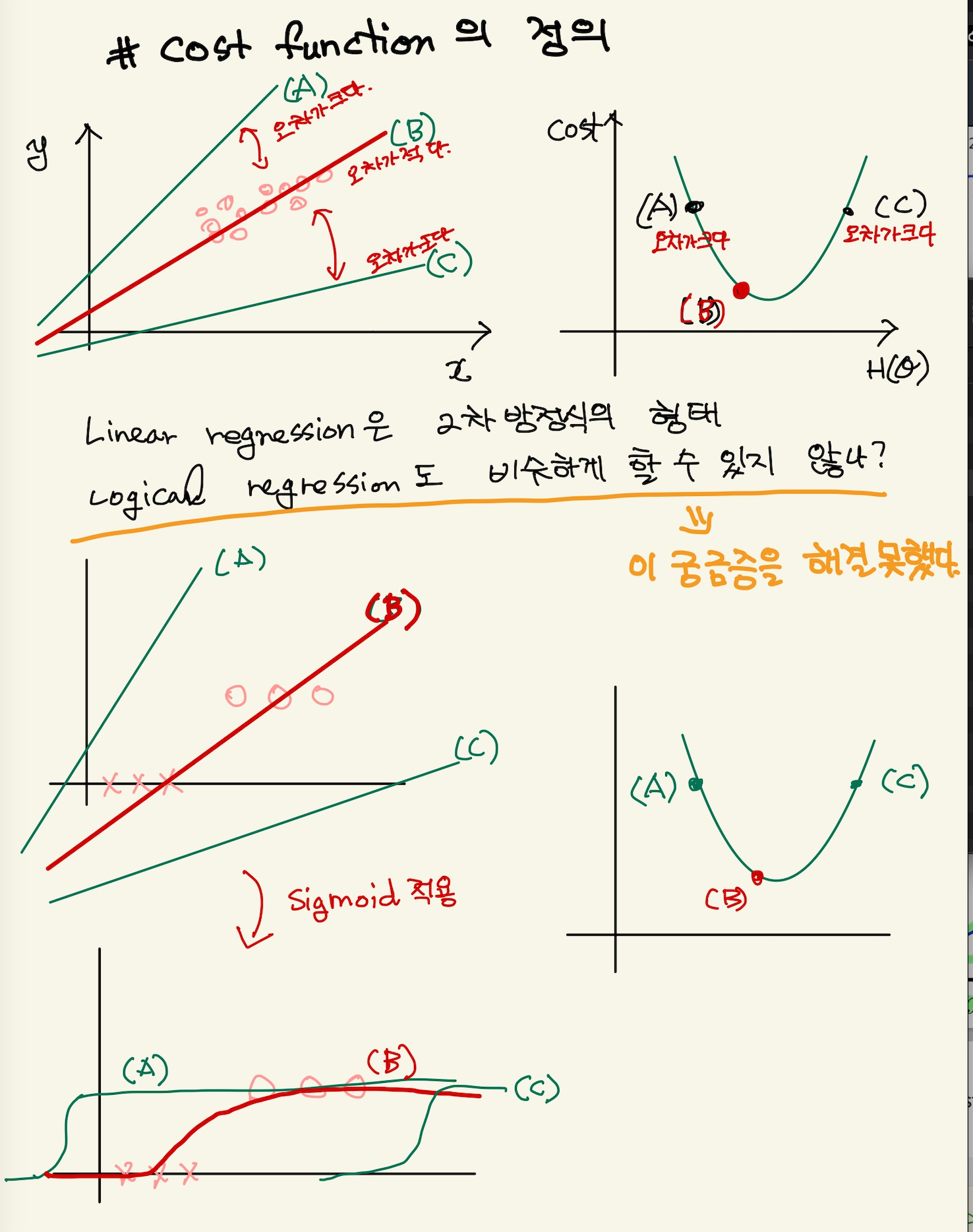
Figure 14: classification_4
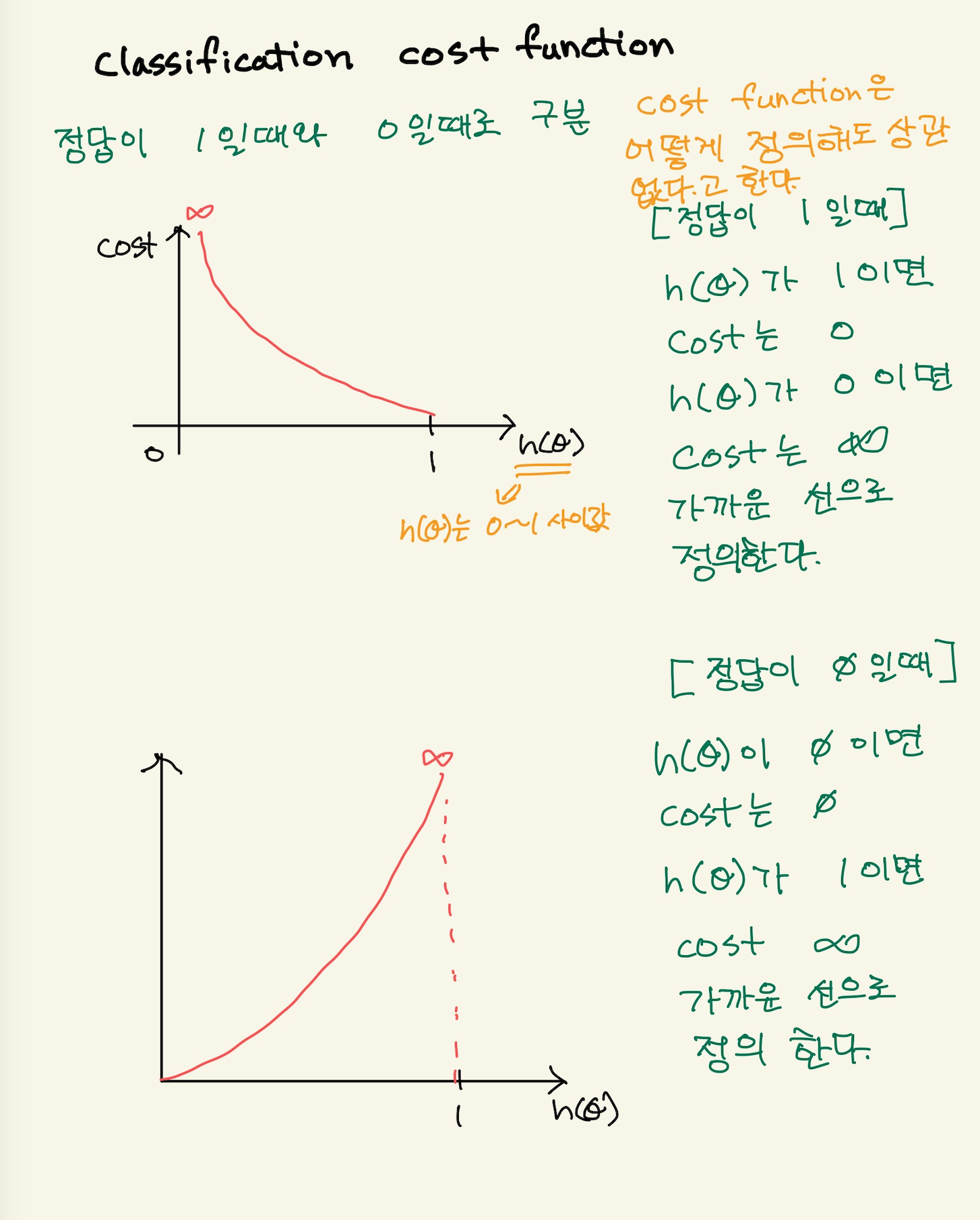
Figure 15: classification_5
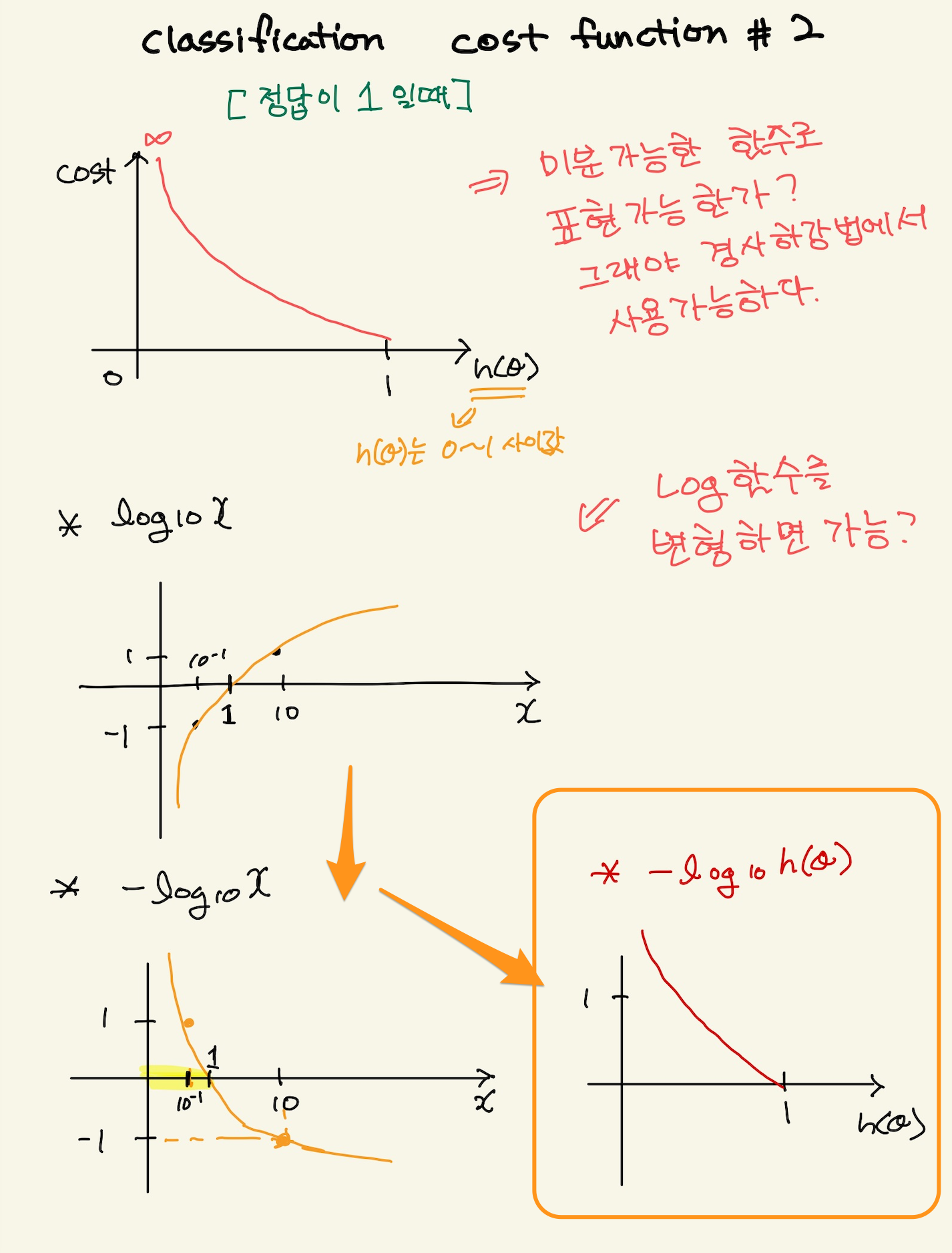
Figure 16: classification_6
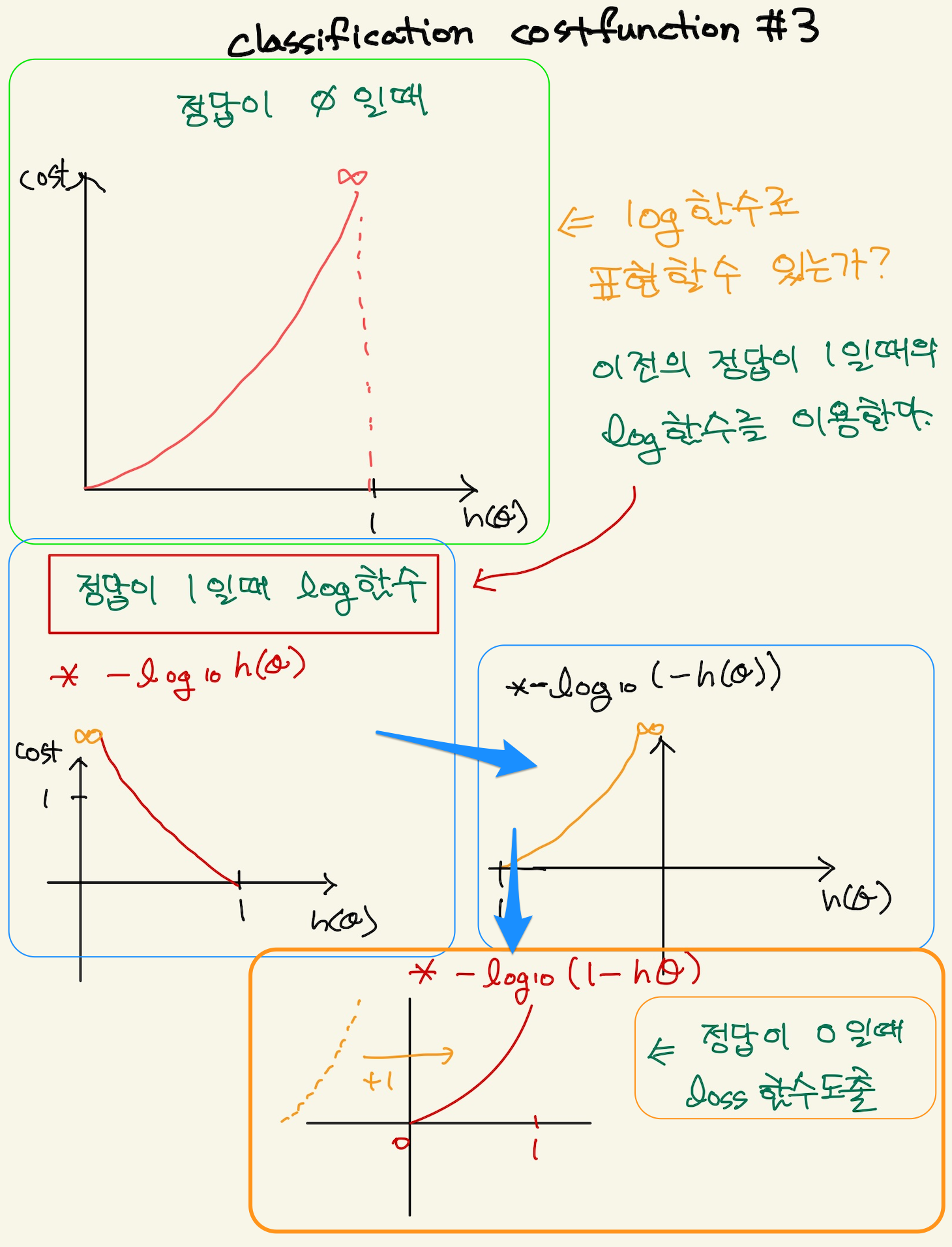
Figure 17: classification_7
cost function이란게 꼭 linear regression처럼 정답-예측치의 제곱형태로 나타낼 필요는 없다. 오차함수는 오차를 잘 표현하기만 하면 된다. 즉, 정답과 예측치의 차이를 오차로 표현 할수도 있지만, classfication같은 경우, 둘중 하나다. 정답과 예측치가 같으면 loss는 0, 만일 다르면 오차는 30 혹은 50 무한대, 마음껏 정할 수가 있는것이다. 오차를 잘 표현만 하면 되는 것이다. 파라미터가 정해지고 데이터가 주어졌을 때 오차함수는 오차함수를 잘 나타내기만 하면된다. 기울기와 같은 parameter를 포함하는 식으로 나타내기만 하면 된다. 그래서 classification에서 오차함수를 log함수로 나타낸 것이다. 이건 아무 문제가 없는 것이다.
그리고 cost function에 대한 정의가 좀 애매한데, linear regression은 오차함수를 데이터셋에 대해 모두 오차를 구한 평균값을 cost function이라고 불렀는데, logical regression에서는 오차함수가 있기 때문에,오차함수를 모든 dataset에 계산하는 식을 그냥 $J(θ)$라고 한다. 내 생각에 cost function은 linear regression에서는 정답-오답의 제곱을 말하는거 같다. logical classification에서 cost function은 log함수를 말하는거 같다. 여튼 linear regression이나 logical regression이나 모두 dataset에 대해서 평균 오차를 구하는 식을 별도로 J(θ)라고 나타내는 듯하다.
log 함수로 표현된 오차함수는 정답이 0일때와 정답이 1일때의 그래프로 다르게 표현했다.
\begin{equation} Cost(H_{\theta}(x),y) = \begin{cases} -log(h_{\theta}(x)) & if y=1 \\ -log(1-h_{\theta}(x)) & if y=0 \end{cases}\end{equation}
이것을 하나의 함수로 만들 수 있다. y가 1인 경우, y를 곱하고, y가 0인경우 (1-y)를 곱한 식이다.
\(\text{Cost(h_{\theta}(x),y) =\) \(-ylog(h_{\theta}(x))\) \(-(1-y)log(1-h_{\theta}(x)\)
여기서 y에 1을 대입하면, y가 1일때의 cost함수가 나온다. y가 0일때는 y가 0일때 cost가 나오는 것을 확인할 수 있다.
gradient descent
gradient discent를 나타내기 위해서 우선 평균 오차함수 $j(θ)$를 표현해야 한다. 평균 오차함수는 위에서 정의된 오차함수를 모든 dataset에 적용한 후 평균을 내는 것이다. linear regression에서 cost function이 정답과 오차의 차로 정의된다면 logical regression에서의 cost function은 정답과 오차의 곱으로 나타내진다. 여튼 평균 오차함수는 다음과 같다.
\(J(h_{\theta}) =\) \(- \cfrac{1}{2n}\) \(\sum_{i=1}^{n}\) \(ylog(h_{\theta}(x))\) \(+(1-y)log(1-h_{\theta}(x)\)
예시
예를 들어보자. 우선 모델을 보자. 선형결합으로 된 식이 있고, sigmoid로 연결되어 있다.
\(z= ax+b\), \(y=g(z)\)
cost함수는 a=2, b=-5의 기울기를 가지고 있고, x가 3일때 정답이 1이라고 하자. 그럼
\(z = 2x-5\) , \(x=3\) \(z = 1\)
\(y = g(1)\)
sigmoid가 1일때의 값은 대략, 0.7정도 된다. 이것이 예측치가 된다.
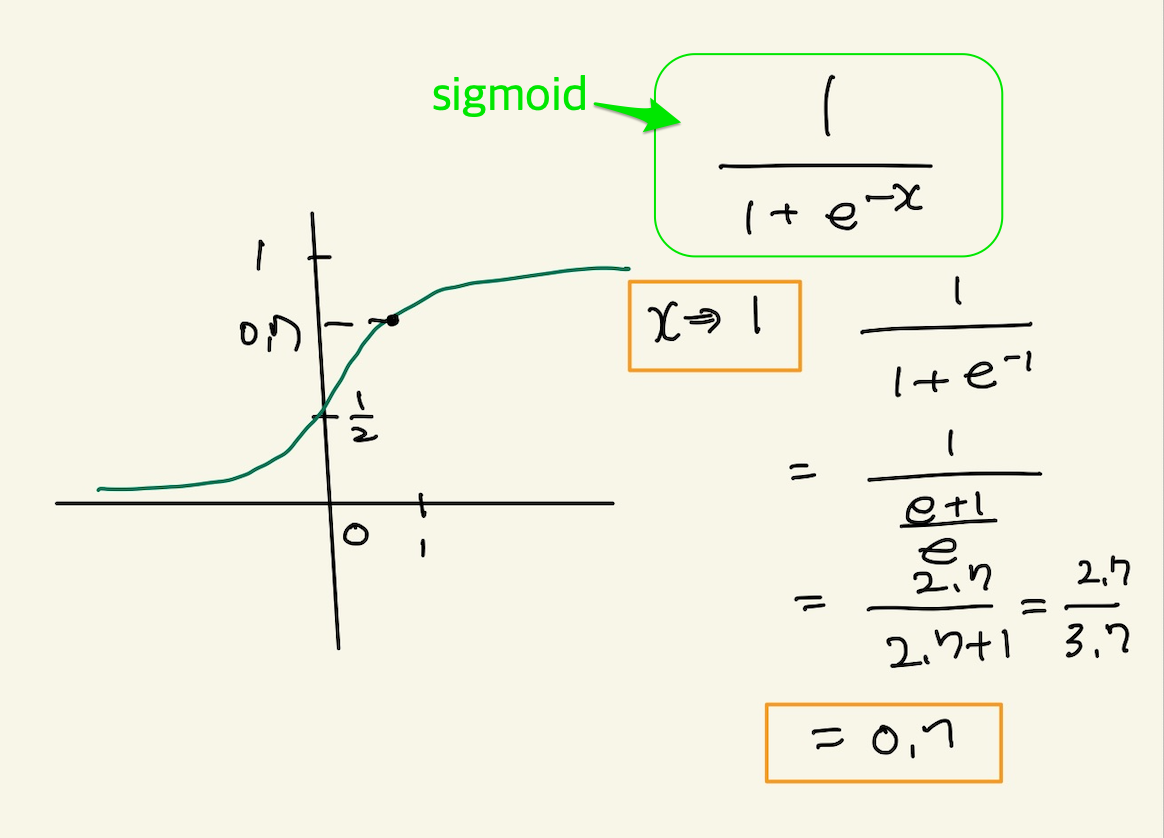
Figure 18: logical gradient descent2
정답이 1일때 오차함수는 아래와 같은 그래프를 갖는다.
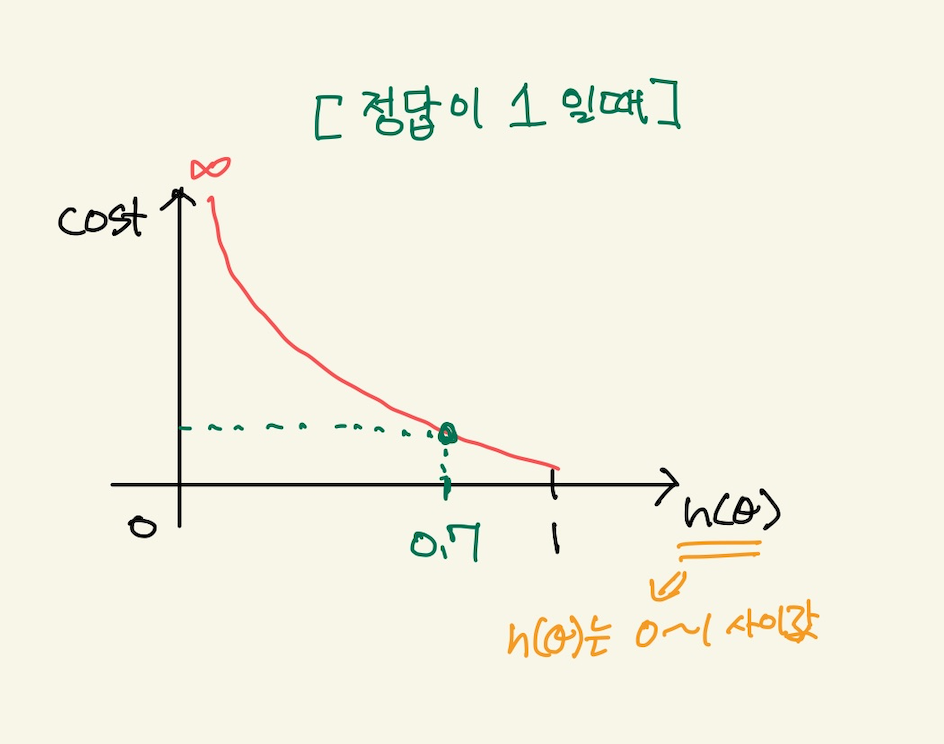
Figure 19: logical gradient descent3
loss가 0이 아니기때문에 기울기를 update 해줘야 한다. y가 1일때 log함수는 다음과 같다.
\(cost(h(x))=\) \(-log(h(x))\) , \(h(x)=\) \(\cfrac{1}{1+e^{ax+b}}\)
\(\text{J(a,b)}=\) \(-log(\cfrac{1}{1+e^{-(ax+b)}})\)
여기서 a,b에 대해서 편미분 한후 해당 data를 입력하면 미분값을 얻을 수 있게 된다. 편미분을 해보자.
\(\cfrac{dJ(a,b)}{da}=\)?
위의 함수는 log의 합성함수다. log함수 미분법을 알아야 한다.
\((log_{e}x)^{’} =\) \(\cfrac{1}{x}\)
그리고 log를 미분한 후 안에 있는 분수 함수도 미분해야 한다. 분수 함수를 미분해보자.
\(Z =\) \(\cfrac{1}{1+e^{-(ax+b)}}\)
\(S =\) \(1+e^{-(ax+b)}\)
\(Z=\) \(\cfrac{1}{S}\)
\(Z^{’}=\) \(-\cfrac{1}{S^{2}}\) \(S^{’}\)
\(= \cfrac{1}{(1+e^{-(ax+b)})^{2}}\) \(-e^{-(ax+b)}\) \(x\)
따라서 다시 식을 쓰면,
\(\cfrac{dJ(a,b)}{da}=\) - \(\cfrac{1}{\cfrac{1}{1+e^{-(ax+b)}}}\) x - \(\cfrac{1}{(1+e^{-(ax+b)})^{2}}\) x \(-e^{-(ax+b)}\) x \(x\)
\(= \cfrac{1}{(1+e^{-(ax+b)})}\) x \(-e^{-(ax+b)}\) x $x$n
\(= \cfrac{-e^{-(ax+b)}}{(1+e^{-(ax+b)})}\) x \(x\)
\(= -\) \(\cfrac{e^{-(ax+b)}}{(1+e^{-(ax+b)})}\) x \(x\)
강사는 여기서 위 식을 해석할 수 있어야 한다고 말한다. 위에서 관심을 갖는건 x에 곱해지는 계수같은 식이다. 이 식이 sigmoide와 비슷한데, sigmoid를 해석하듯이 해야 한다고 한다.
\(\cfrac{e^{-(ax+b)}}{(1+e^{-(ax+b)})}\) , \(z =\) \(-(ax+b)\)
= \(\cfrac{e^{z}}{(1+e^{z})}\)
-(ax+b)를 z로 치환하고 정리하면 sigmoid와 비슷한형태가 나온다. 위식이 왜 sigmoid하고 비슷한지는 아래를 보자.
sigmoid= \(\cfrac{1}{1+e^{-x}}\)
여기서 \(e^{x}\) 를 위아래 곱하면
\(\text{sigmoid} =\) \(\cfrac{1}{1+e^{-x}}\) \(\cfrac{e^{x}}{e^{x}}\)
\(=\cfrac{e^{x}}{e^{x}+1}\)
\(=\cfrac{e^{x}}{e^{x}+e^{0}}\)
위에서 치환한 식과 같다. 그러면 시그모이드의 의미가 무엇인가? 강사는 분모와 분자에 2개의 지수승이 있는데, 이것이 비율을 뜻한다고 한다. 즉 $ex$와 e0 에서 $ex가 1에 대한 비율이라는 것이다. 지수는 ax+b인데, 이것은 선형결합해서 나오는 값이다. 이값이 2.7이면 2.7의 상대적인 비율은 다음과 같다.
\(\cfrac{2.7}{1+2.7}\)
즉, sigmoid라는게 상대적인 비율을 가리키기 때문에 우리가 치환한 z도 비율을 뜻한다고 해석할 수 있다. z가 0일경우, e0과 비율이 같다. 이것은 sigmoid에서 50%와 동일하다. 만일 z가 0보다 크다면, e0보다 상대적인 비율이 크니까, 큰값이 나올텐데, 이것은 sigmoid가 1/2보다 큰값이 나온다고 해석할 수 있다. 즉 비율을 따지는게 sigmoid의 의미라는 것이다. 상대적인 비율을 말하는 이유는 sigmoid를 안써도 직관적으로 알수 있기 때문이다. 예를들어 ax+b가 0이 나왔다면, 아..1과 1의 상대적인 비율이 같기 때문에, 1/1+1에 의해 sigmoid가 50%값을 내놓을거라고 예측할 수 있다. 만일 ax+b가 1이면, 2.7/2.7+1 은 대략적으로 66%라고 예측할 수 있는것이다. sigmoid 안쓰고 암산이 가능하다.
근데 전체적으로 너무 어려웠다. 이해하기 너무 힘들어서 pass한다.
그러면 gradient descent는 새로운기울기를 구하는건데 공식은 어떻게 되나?
새로운 기울기 = 이전 기울기 - \(\alpha\) \(\sum_{1}^{m} 예측치 - 정답\)
맞는지는 모르겠지만, 너무 어렵고 이것에 시간을 너무 많이 투자한거 같아서 pass한다. 강사가 나중에 이런 loss function을 cross entrophy라고 말을 했는데 잘 모르겠다.
Multi-class classification
one vs all 기법
예를들어보자. 우리가 가진 data는 사진 데이터다. 개, 고양이, 사람 사진들을 가지고 있다. 어떤 사진을 주었을때 개인지 고양인지 사람인지를 맞추는 multi-class classification을 구현하려고 한다. 어떻게 해야 할까? binary classification을 이용한다. 다음과 같은 feature space가 있다고 하자.
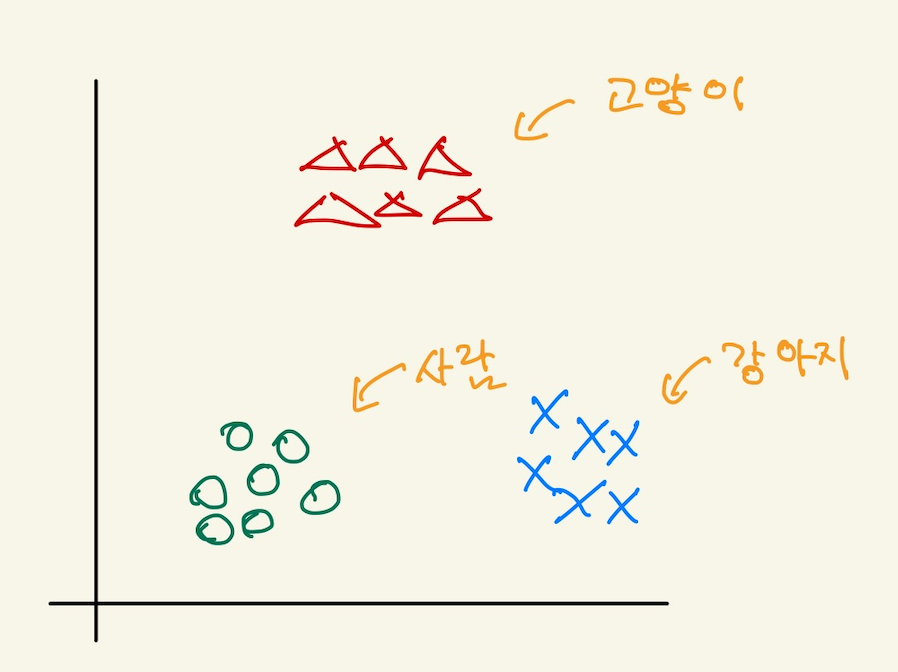
Figure 20: multi1
우리는 1개의 모델이 아닌 3개의 binary classification model을 만든다. 각각의 모델은 하나만을 인식할 수 있다. 예를 들어서, 강아지만 분류하는 model, 고양이만 분류하는 모델, 사람만 분류하는 모델을 만들어서 훈련시킨다.
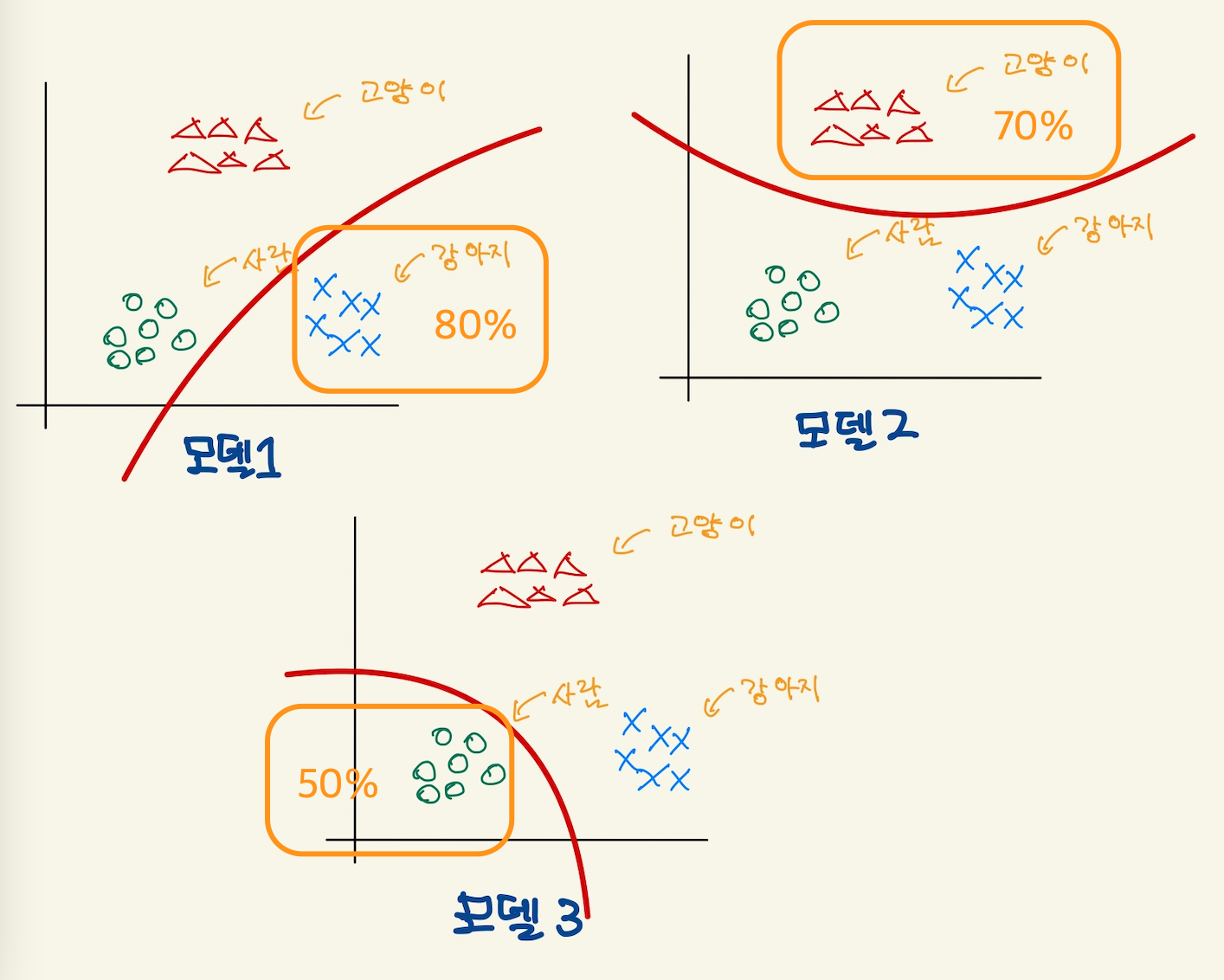
Figure 21: multi2
그리고 어떤 사진을 3개의 모델에 입력해서 나온 확률값들 중에 가장 큰 모델을 선택하는 방식이다. 즉 3개의 모델이 하나의 multi classification model이라고 볼 수 도 있다. 위에선 강아지를 선택한 값이 가장 높기 때문에 강아지를 예측값으로 도출한다.
softmax function
각각의 model의 결과값을 비교해서 값이 놓은 확률을 갖는 모델을 선택하는 방식은 각각의 모델별로 다른 확률값을 출력한다. 위에서 봤듯이 강아지 80%, 고양이 70%, 사람 40% 등등…그런데 softmax를 사용하면 각각의 모델별 계산을 하나의 확률로 표현할 수 있게 된다고 한다. 즉 강아지 60% 고양이 30% 사람 10% 라는 하나의 확률로 나타낼 수 있다고 한다. 합이 100%인 노멀라이즈된 형태로 나온다. sigmoid보다 softmax가 더 자연스럽고, 딥러닝에서 많이 사용된다고 한다.
다시 정리 필요
우리가 만든 logistic model은 두개 함수로 이루어진 합성함수다. linear regression에 사용되는 직선과 sigmoid 함수다. 나는 linear regression 함수가 decision boundary가 아닐까 하는 생각을 했었다. 하지만 모르겠다. 예를 들어, 우리가 위의 data에 대한 classification model을 만들어서 최적의 machine을 만들었다고 하자. 최소의 오차를 갖는 최적의 machine이기 때문에, linear regression의 직선은 위와 같은 decision boundary의 모양일 거라 생각했다. 그런데 아래와 같은 형태로 볼 수 있다. 왜냐면 이 형태가 linear regression에서 최소의 오차를 갖는 직선이기 때문이다. 그런데 linear regression과 달리 classification의 최소 오차의 합을 구하는 식은 sigmoid가 있기때문에 계산식이 다르다. linear regression직선을 최소 오차의 합으로 그리면 안되고, 아래그림의 오른쪽처럼 sigmoid가 포함된 hypotheis function의 오차의 합의 최소값을 갖는 sigmoid가 그려질때 좌측의 직선이 결정되기 때문이다. 따라서 위의 x=4라는 직선이 그 때 당시의 linear regression직선일 수도 있는것이다. 내가 classification model에서 linear 1차방정식이 decision boundary라고 생각한것은 나중에 보겠지만, 비슷한 설명이 나오기 때문이다. 그리고 실제 아래에서 sigmoid곡선이 최적이 machine을 찾은후 그때, 1차방정식은 아래 그림의 왼쪽 그림이 아닌, 위에 그림일 수도 있다. 그래서, 아직은 잘 모르겠다.
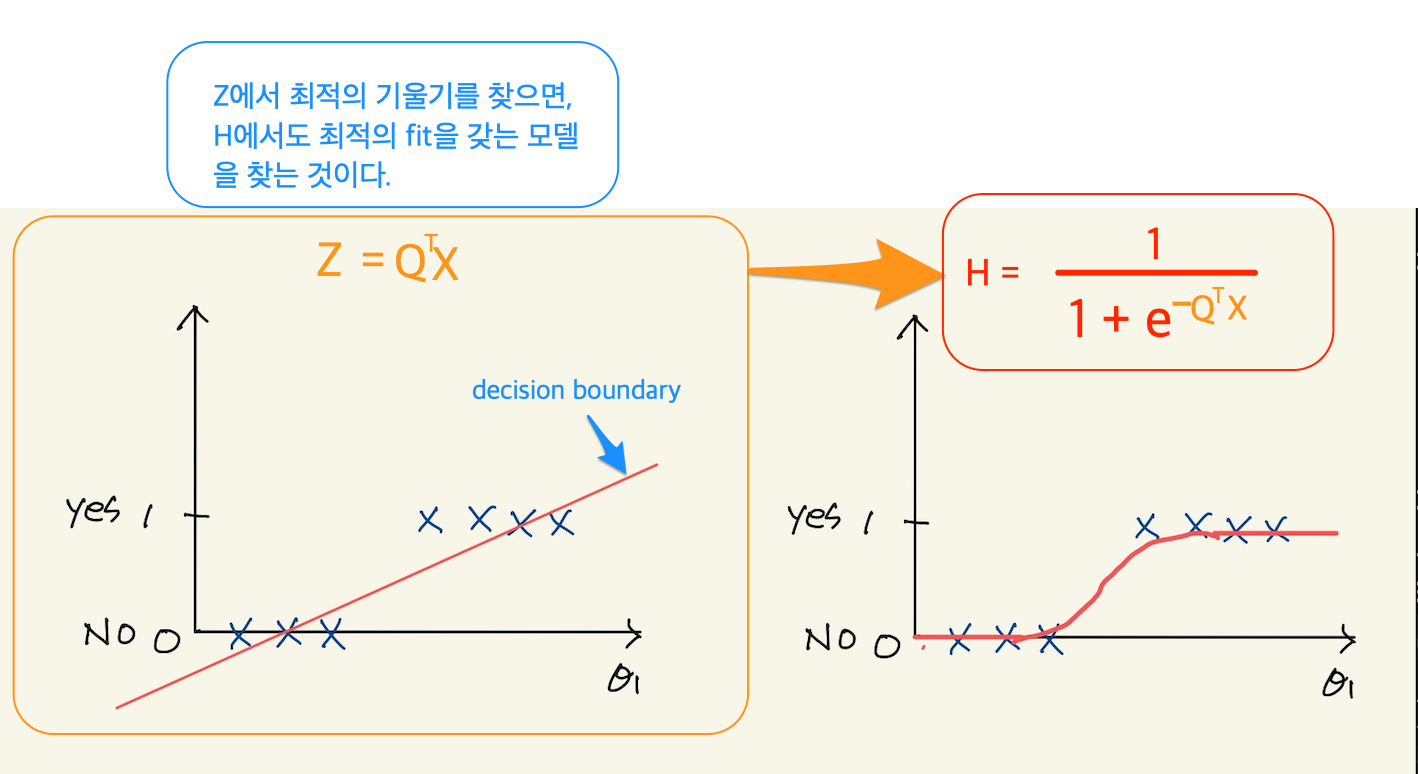
Figure 22: logical decision boundary1
즉 1차함수와 sigmoid를 나누어 봤을때, 1차함수는 feature space에서 일종의 decision boundary역할을 한다고 보기로 하자. 그러면 위의 그림에서 좌측을 생각하면 안된다. 계산을 직접하기 전까지는 모르기 때문이다. x=4라는 직선일 수도 있다.
feature가 여러개인 multi-variables classification
feature가 2개인 경우도 비슷하게 볼 수 있다. 2개의 feature로 된 data를 feature space로 나타내면, 2개로 양분 시키는 decision boundary를 볼 수 있다. model에는 2개의 함수가 합성함수로 되어 있다고 보면, 그중 첫번째 있는 1차함수가 decision boundary를 나타낸다고 본다. 강사의 설명이 그런식이다. 위에서는 내가 확실치 않다고 하긴 했다.
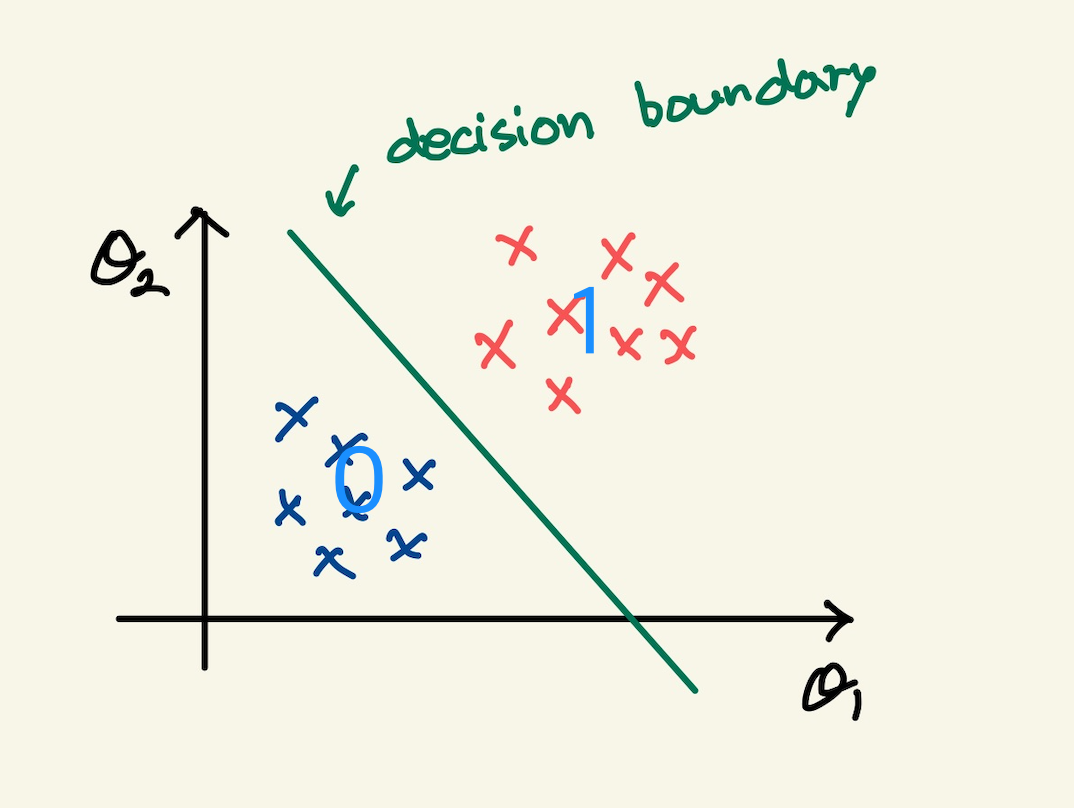
Figure 23: logical decision boundary2
non-linear decision boundary
decision boundary를 나타내는게 model의 첫번째 함수라고 하자. 이 첫번째 함수인 decision boundary는 여러가지 모양으로 나타낼 수 있다고 이전 polynomial regression과 decision boundary에서 말한바 있다. 즉 linear regression에서 model은 직선형태만 나타내는게 아니라, feature로 제곱근이 있는 식을 추가하면 완만한 곡선을 표현했고, 제곱을 추가해서 위로 급격히 상승하는 그래프를 만들 수 있었다. 이렇게 다양한 모양의 그래프를 만드는 이유는 단 하나 data분포가 그렇기 때문이다. 그렇다면 다음과 같은 decision boundary를 생각해보자.
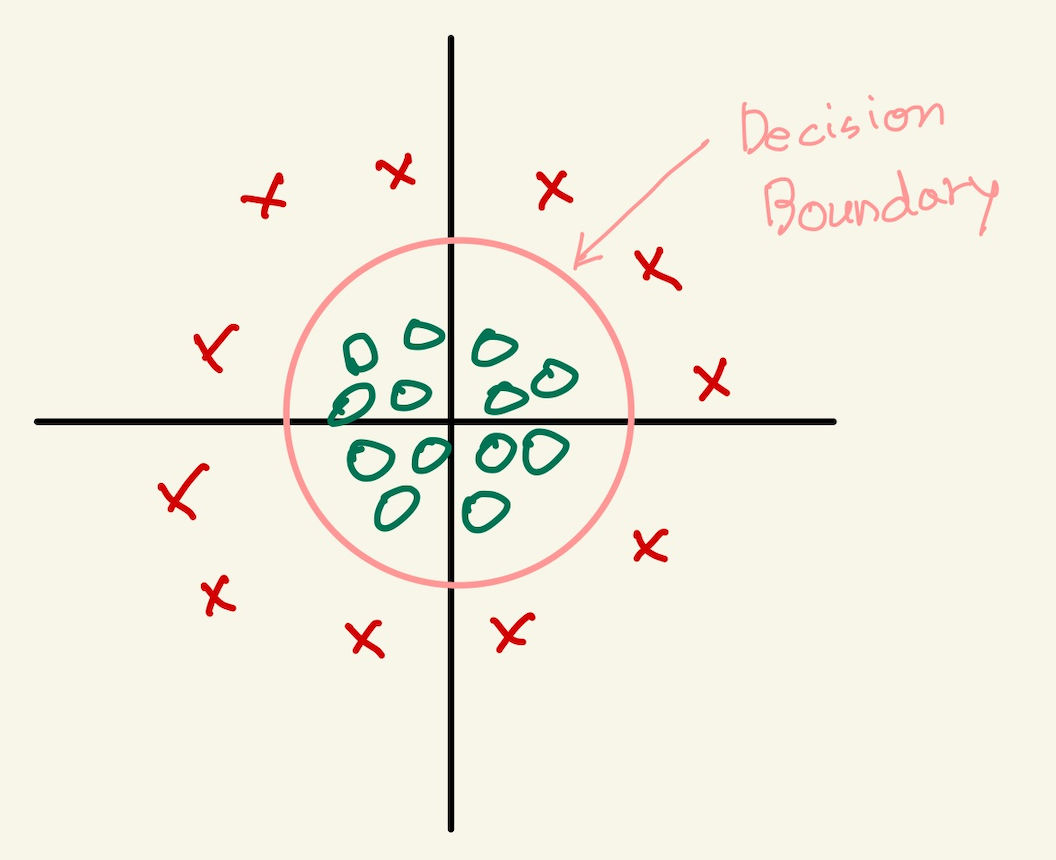
Figure 24: circle
decision boundary는 원의 형태다. 직선형태가 아니기 때문에 non-linear decision boundary라고 할 수 있다. 그런데 이것의 hypotheis function은 다음과 같은 형태다.
\(h_{\theta}(x) =\) \(g(\theta_{0}\) \(+ \theta_{1}x_{1}\) \(+ \theta_{2}x_{2}\) \(+ \theta_{3}x_{1}^{2}\) \(+ \theta_{4}x_{2}^{2})\)
hypotheis function에서 g함수는 sigmoid function이고, 안이 linear regression형태의 직선이였는데, 마치 polynomial regression에서 변종된 형태처럼 원의 방정식으로 되어 있다.
옛날cost function
1차함수의 예측값은 sigmoid의 도움으로 0-1사이의 값을 갖게 되고, 정답과 예측의 차이를 나타내는 loss function은 2차 함수가 아니게 된다.왜냐면 예측하는 hypotheis function이 다음과 같은 지수함수이기 때문이다.
\(H =\) \(\cfrac{1}{1+e^{-Z}}\) \(= \cfrac{1}{1+e^{-(Q^{T}X})}\)
그러면 loss function은 정답과 hypotheis function의 차에 제곱을 한 형태를 모든 data를 입력해서 나온값을 더하는 형태다. 정답과 hypotheis function의 차는 지수함수다. 지수함수의 제곱도 지수함수다. 이런 지수함수들을 모든데이터를 넣어서 합한것도 지수함수가 된다. 그럼 경사하강법에 사용되는 미분식은 지수를 미분한 log함수가 될 거라고 예상이 된다.
이해한것과 의문점
어떤 data가 있다. 그 데이터를 yes or no로 분류하고 싶다. 예를 들어, 메일의 제목,날짜, 크기같은 data를 보고 spam인지 아닌지를 판단한다던지, 종양의 크기나 모양과 같은 수치 데이터를 보고 악성인지 양성인지를 판단하는 문제를 machine learning으로 풀고 싶다.
주어진 data에 따른 정답이 주어져 있다. training data이기 때문이다. yes or no나 양성 혹은 악성은 2개의 정답을 갖는다. 이것을 값으로 표현을 해야 한다. 가장 쉬운건 0과 1이라고 하는 것이다.
| 크기 | 모양 | 결과 |
|---|---|---|
| 32 | 2.3 | 양성 |
| 33 | 3.1 | 양성 |
| 15 | 1.5 | 악성 |
| 33 | 1.8 | 악성 |
| 크기 | 모양 | 결과 |
|---|---|---|
| 32 | 2.3 | 1 |
| 33 | 3.1 | 1 |
| 15 | 1.5 | 0 |
| 33 | 1.8 | 0 |
위의 dataset을 학습한 후 결과값이 없는 data의 결과값을 예측하는 것이다. 크기와 모양의 data가 주어지면 결과를 예측하고 싶다. 예측한다는 것은 machine learning으로 해결할 수 있다. 따라서 machine learning을 만든다. machine에 해당하는 function(model)과 learning, 즉 update하는 cost function, 두개 function을 만들어야 한다. 우리가 지금껏 배운것은 1차방정식 밖에 없다. 그래서 model로 선형결합된 1차방정식을 사용하기로 한다. model은 machine의 function을 말한다. model이 있다면 예측할 수 있다. 바로 예측할 수는 없다. model의 parameter, 즉 1차방정식 계수를 임의로 초기화 해야 한다. 그래야 예측값이 나온다. 지금은 learning을 생각하지 않는다. 여튼 지금 model과 parameter세팅이 끝났기 때문에, machine을 동작시킬 수 있다. machine을 동작시켜보자.
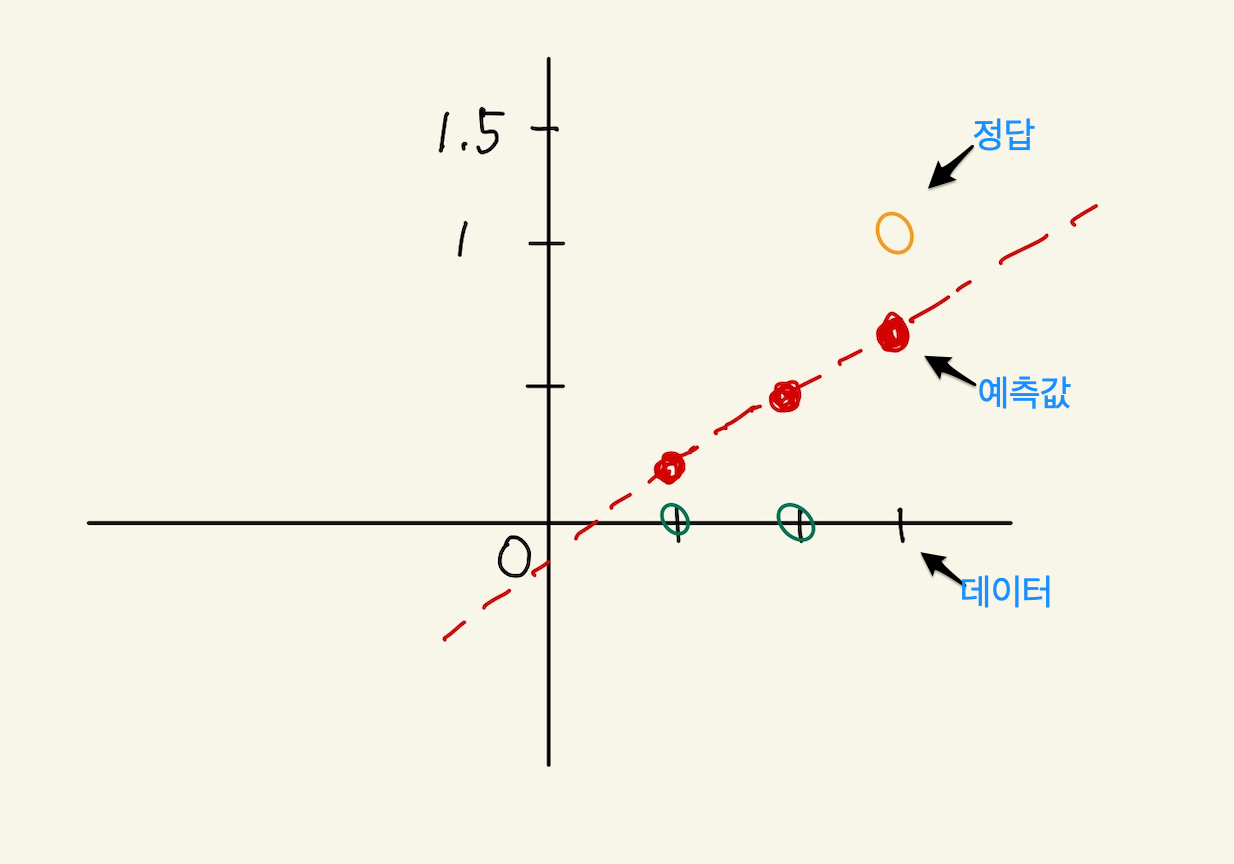
Figure 25: logical regression1
그림이 좀 복잡하다. 여튼, 주황색 직선은 model의 1차 함수다. 1차함수의 결과값이 예측값이다. 처음 model의 계수는 임의의값으로 설정되었기때문에, 예측값은 정답과는 차이가 있다. 오차가 있기 때문에 cost function이 계수를 변경시킬 것이다. 아래 보면 update된 machine들이 보여질 것이다.
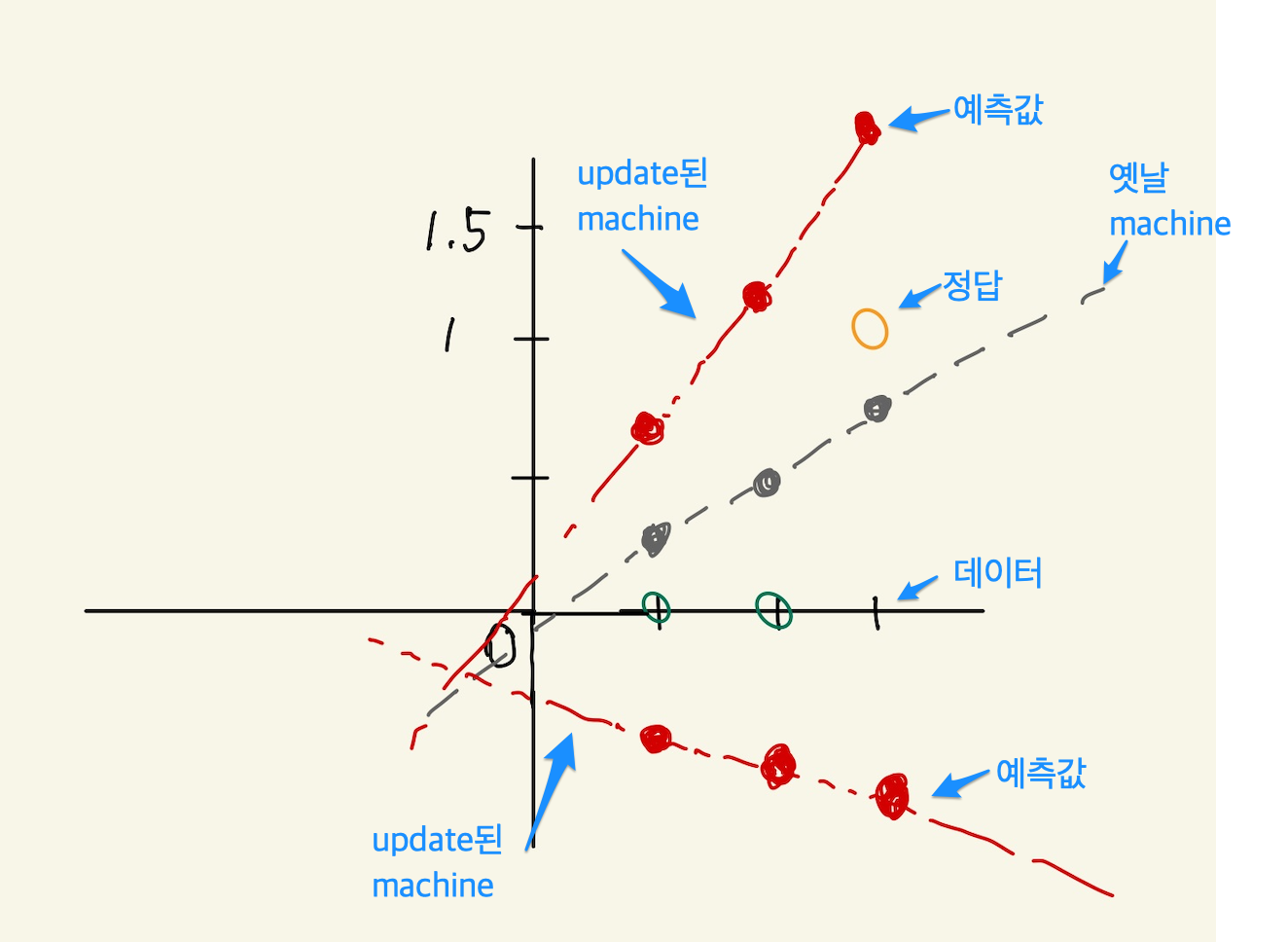
Figure 26: logical regression2
우리가 원하는 건 machine의 예측값이 정답과 같은 machine을 만드는 것이다. 그런데, 그런 machine이 가능할까? 예측값의 분포와 정답의 분포를 보면 알수 있다. 이전의 linear regression에서 보면 정답의 분포는 1차원 직선형태였다. 따라서 machine의 model이 직선이기 때문에 예측이 가능하다는것은 합리적이다. 그런데 classification의 정답의 분포는 1차원 직선형태도 아니고, 출력값이 0과 1로된 data이기 때문에 예측 자체가 불가능하다. 위의 그림을 봐도 직선의 방정식이 update되어서 다양한 방향을 가르켜도 정답의 데이터 분포와 비슷해질 수 없다. 그러면 어떻게 해야 할까?
step function
step function은 다음과 같은 함수다.
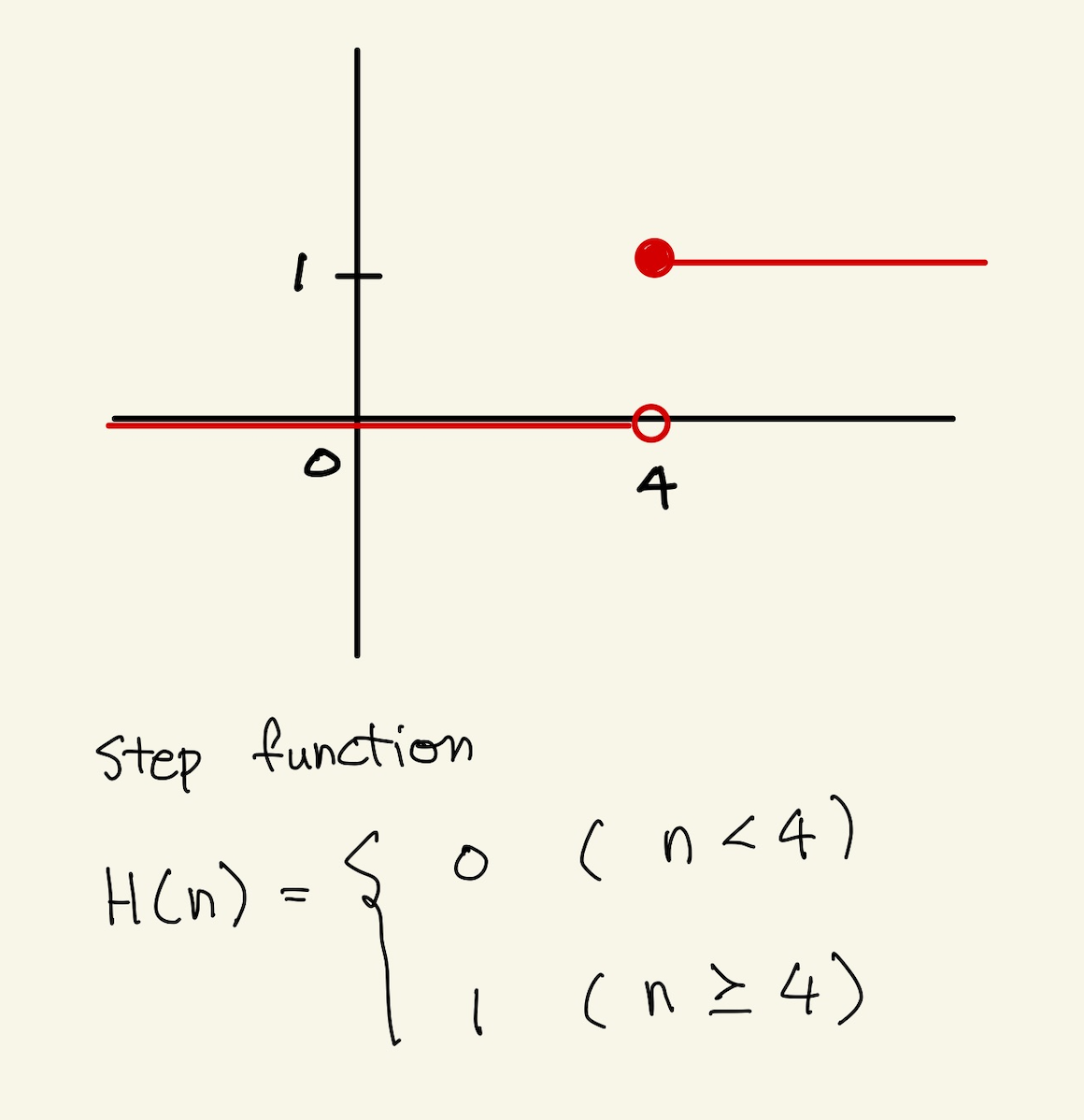
Figure 27: step function
정답의 분포에 맞는 machine은 step function이 가장 잘 어울린다. 그런데 이걸로 model을 만든다고 할때 다변수가 있는 경우 어떻게 모델을 만들것이며 cost function도 어떻게 만들것인가? 설사 cost function을 만든다고 해도 미분이 불가능하다. 즉 cost function을 만들수가 없다.
sigmoid function
정답 분포에 맞는 machine이면서 미분이 가능하다.
sigmoid function을 사용시 의문점
model로 sigmoid function을 바로 사용하는게 아니라, 강사는 model은 1차함수를 그대로 사용하고, sigmoid function을 adapter형식으로 끼워서 사용한다. 즉 함성함수처럼 1차함수로 나온결과에 sigmoid function을 적용한다. 왜 그러는지는 모르겠다. feature가 1개일때는 sigmoid를 써도 되나, feature가 여러개일때는 sigmoid를 사용할수 없기 때문인가?
model을 1차함수 그대로 사용하는 이유
model을 1차원 함수를 사용할때는 model의 예측치가 실수값이다. 그런데 우리가 원하는건 실수값이 아니다. model의 예측치로 나온 실수값 혹은 예측치에 해당하는 직선의 그래프는 분류를 할 수 없다. 정답의 분포를 보면, 분류할 수 있는 함수들 step function이나 sigmoid같은 함수들은 분류를 할수 있어 보인다. 그렇다고 그런 함수를 model로 사용하면 될거 같은데, 강사는 분류가 가능할거 같은 sigmoid나 step function을 model로 사용하지 않는다. 대신, 1차함수 model은 그대로 사용하고 분류할수 있는 sigmoid같은 함수를 adapter형식으로 끼워서 사용한다. 왜 직접 분류가 가능한 함수를 model로 안 사용하고, 1차원 함수를 그대로 사용하는가? sigmoid같은 함수에서 다변수를 표현할 수 있어야 한다. 다변수 만큼의 sigmoid를 사용하던가 다변수를 표현한 식이 sigmoid에 들어가던가 해야할것인가? 다변수를 표시할 수 있어야만 cost함수에서 다변수 각각에 편미분을 적용해서 각각의 계수를 update가 가능하기 때문이다. 다변수만큼의 sigmoid를 사용하는건 불가능한것 같고, 다변수를 포함한 식을 sigmoid에 전달하는 합성함수 형태, adapter 형태만이 cost function이 계수들을 편미분해서 update할수 있게 만드는거 같다.
요약하면 모델로 1차함수를 그대로 사용하는 이유는 cost function때문이다. update할 대상인 계수들이 1차함수로 표시되고 정답과 1차함수값의 차이를 제곱한후 나오는 2차방정식을 편미분할 수 있기 때문이다. sigmoid로 했을때는 다변수를 표시하기가 어려운거 같다. 명확한 해답은 아니다. 1차함수를 사용하지 않으면 update할 께 없다. update할 계수가 1차함수에 있기 때문이다. 따라서 1차함수를 그대로 사용하고 분류하는 함수를 adapter형식으로 끼워넣어서 사용한다.
feature가 1개일때의 예시
위에서도 말했지만 모델에서 1차원 함수를 사용할수 밖에 없다고 했다. 왜냐면, 1차함수가 계수와 data로 이루어진 식이라서 cost function이 계수를 update할 수 있기 때문이다. 즉 1차함수 + adapter를 통해서 예측값을 출력하고, 정답과 예측함수의 차로 cost function을 만들수 있다. 그럼 예를 들어보자.
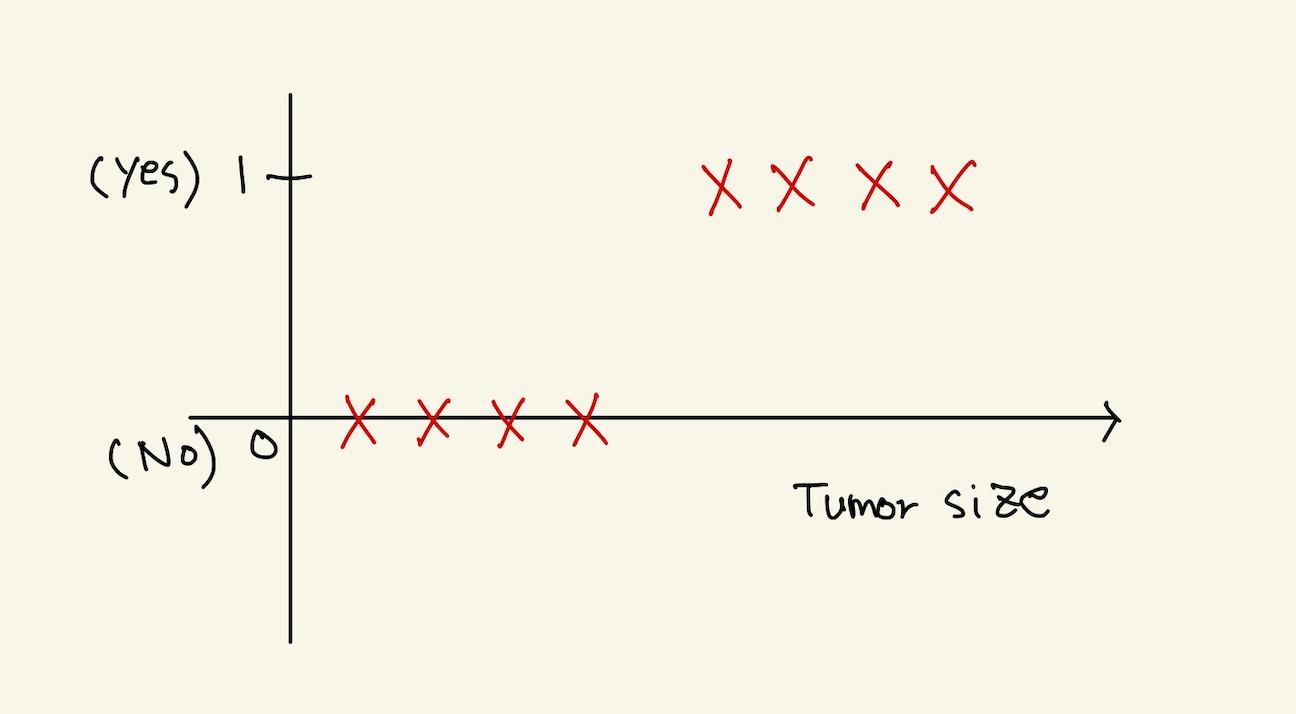
Figure 28: decision boundary1
위 그림은 정답이 0 아니면 1로 되어 있는 분류 문제다. 분류문제는 adapter가 필요하다고 했다. 1차함수로 분류를 할수 없기 때문이다. 그렇다고 1차함수를 안 쓸수도 없다. update가 안되기 때문이다. 어쨋든 1차함수를 써야하는데, 다음과 같은 함수를 사용하기로 하자. 이것은 step function이다.
\(if\) \(h_{\theta}(x)\) \(\ge\) \(0.5\), \(predict “y=1”\) \(if\) \(h_{\theta}(x)\) \(\le\) \(0.5\), \(predict “y=0”\)
최고의 decision boundary는 아래와 같은 그림일 것이다.
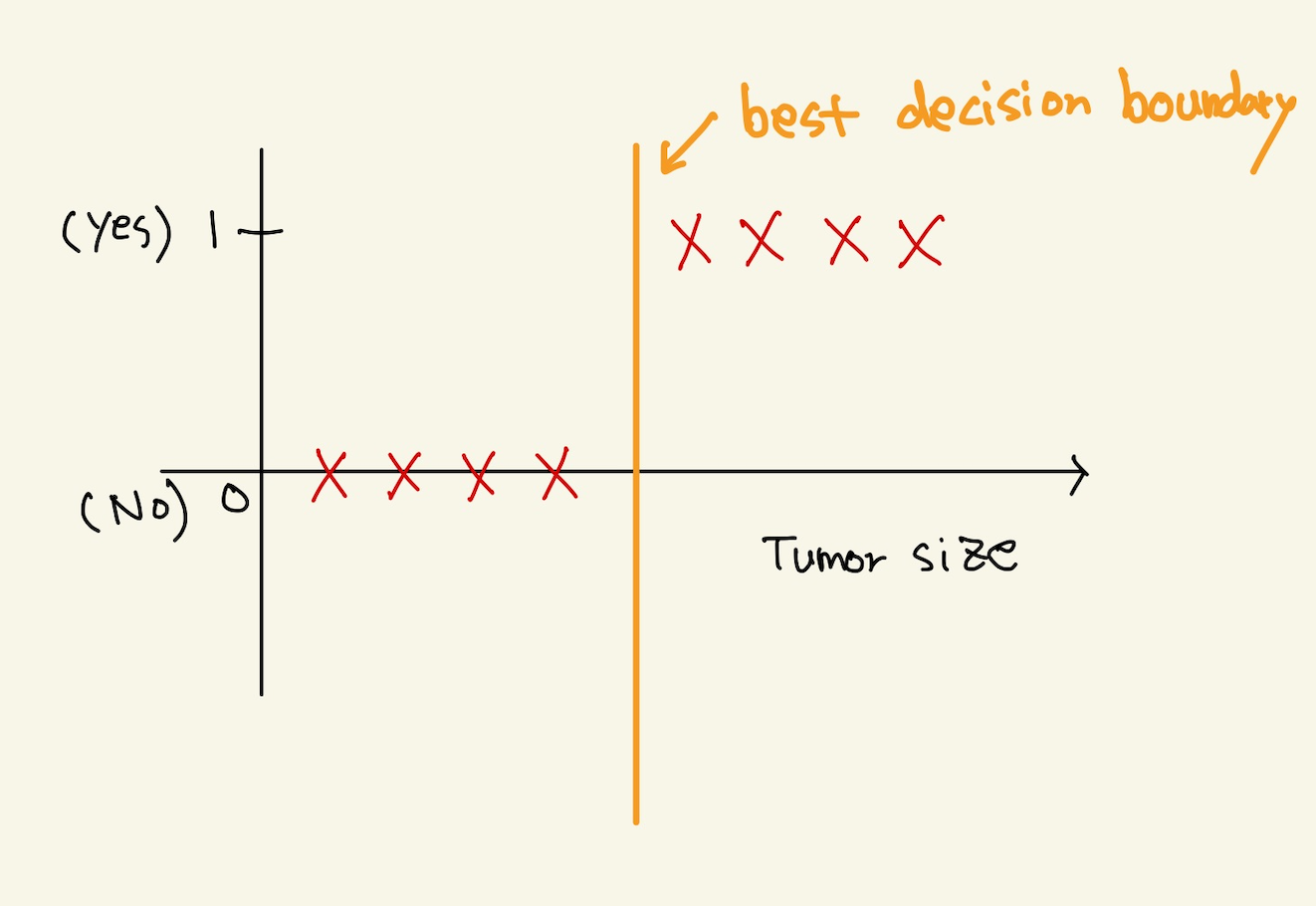
Figure 29: decisionboundary2
그런데 그런 decision boundary는 가질 수 없다. 왜냐면 cost function에 의해서 decision boundary가 계속 움직이는데, 저런 직선이 되려면, cost function이 무한의 오차를 가져야한다. cost function은 오차를 적게 하는쪽으로 이동하기때문에 저런 직선은 나올 수가 없다.
